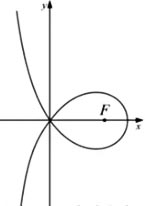
造型  可以做成美丽的丝带,将其看作图中曲线C的一部分.已知C过坐标原点O,且C上的点满足:横坐标大于-2,到点F(2,0)的距离与到定直线x=a(a<0)的距离之积为4,则【 】
可以做成美丽的丝带,将其看作图中曲线C的一部分.已知C过坐标原点O,且C上的点满足:横坐标大于-2,到点F(2,0)的距离与到定直线x=a(a<0)的距离之积为4,则【 】
A、a=-2
B、点(2√2,0)在C上
C、C在第一象限的点的纵坐标的最大值为1
D、当点(x0,y0)在C上时,y0≤4/(x0+2)
造型  可以做成美丽的丝带,将其看作图中曲线C的一部分.已知C过坐标原点O,且C上的点满足:横坐标大于-2,到点F(2,0)的距离与到定直线x=a(a<0)的距离之积为4,则【 】
可以做成美丽的丝带,将其看作图中曲线C的一部分.已知C过坐标原点O,且C上的点满足:横坐标大于-2,到点F(2,0)的距离与到定直线x=a(a<0)的距离之积为4,则【 】

A、a=-2
B、点(2√2,0)在C上
C、C在第一象限的点的纵坐标的最大值为1
D、当点(x0,y0)在C上时,y0≤4/(x0+2)
ABD
【解析】
解答过程见word版