高中数学-高考试题(上海市 2010年三角函数的诱导公式)

计算题（2010年上海市）

已知0<x<π/2，

简化： lg⁡(cos⁡x•tan⁡x+1-2sin²⁡(x/2))+lg⁡[cos⁡( x-π/4)]-lg⁡( 1+sin⁡2 x).

答案解析

原式=lg⁡(sin⁡x+cos⁡x)+lg⁡(sin⁡x+cos⁡x)-lg⁡(1+sin⁡2 x)

=lg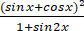

=lg⁡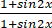

=0

讨论

高中数学

某人要作一个三角形，要求它的三条高的长度分别是1/13 ，1/11 ，1/5 ，则此人将【】

若x0是方程(1/2 )x=x1/3的解，则x0属于区间【】

直线L的参数方程式(t∈R)，则 L的方向向量d可以是【】

“x=2kπ+π/4（k∈Z）”是“tanx=1 ”成立的【】

从集合U={a,b,c,d}的子集中选出4个不同的子集，需同时满足以下两个条件(1) Φ ,U都要选出(2) 对选出的任意两个子集A和B，必有A⊆B或A⊇B.那么，共有_____种不同的选法.

如图所示，直线x=2 与双曲线 Γ: x2/4 - y2=1的渐进线交于E1, E2两点，记=e1,=e2.任取双曲线Γ上的点P，若 = ae1+be2 （a,b∈R)，则a,b满足的一个等式是_______.

如下图所示,在边长为4的正方形纸片ABCD中，AC与BD相交于O，剪去△AOB, 将剩余部分沿OC,OD折叠，使OA,OB重合，则A(B),C,DCO为顶点的四面体的体积是_______.

将直线l1：nx+y-n=0 , l2：x+ny-n=0(n∈N*）， x轴，y轴围成的封闭区域的面积记为Sn，则Sn= ________.

在n行n列矩阵中，记位于第i行第j列的数为 aij (i,j=1,2,...,n).当n=9时，a11+a22+a33+...a99=________.

从一副混合后的扑克牌(52张)中，随机抽取1张，事件A为“抽得红桃K”，事件B为“抽得黑桃”，则概率P(A∪B)= ________(结果用简分数表示).

三角函数

设函数f(x)=sinx+cosx(x∈R).(1)求函数y=[f(x+π/2)]2的最小正周期;(2)求函数y=f(x)f(x-π/4)在[0,π/2]上的最大值.

解方程：sinx+cosx-1=0

证明：(sin2α+1)/(1+cos2α+sin2α)=1/2 tanα+1/2.

设f(x)=sin4⁡x-sinxcosx+cos4⁡x，则f(x)的值域是__________________.

记△ABC的内角A，B，C的对边分别为a，b，c，已知cos⁡A/(1+sin⁡A )=(sin⁡2B)/(1+cos⁡2B)．（1）若C=2π/3，求B；（2）求(a2+b2)/c2 的最小值．

角α,β满足sin⁡(α+β)+cos⁡(α+β)=2√2 cos⁡(α+π/4)sin⁡β，则【】

记函数f(x)=cos⁡(ωx+φ) (ω>0,0<φ<π)的最小正周期为T，若f(T)=√3/2，x=π/9为f(x)的零点，则ω的最小值为____________．

已知函数f(x)=cos2⁡x-sin2⁡x，则【】

若函数f(x)=Asin⁡x-√3cos⁡x的一个零点为π/3，则A=________；f(π/12)=________．

若3sin⁡α-sin⁡β=√10,α+β=π/2，则sin⁡α=__________，cos⁡2β=_________．

三角函数的诱导公式

用公式 cos⁡(θ/2)=±时，式中的正负号怎样决定?

若0<α<β<π/4,sin⁡α+cos⁡α=a,sin⁡β+cos⁡β=b，则【】

若α∈(0,π/2),tan2α=cosα/(2-sinα)，则tanα=【】

cos2 π/12 - cos2 5π/12=【】

求证：(sinα+sinβ)/sin⁡(α+β)=cos((α-β)/2)/cos((α+β)/2)

计算：sin 4π/3∙cos 25π/6∙tg(-3π/4).

已知x+x-1=2cosθ，求证：xn+x-n=2cosnθ.

不查表求sin105°的值.

设函数f(x)=sin⁡(ωx+π/3)在区间(0,π)恰有三个极值点、两个零点，则ω的取值范围是【】

记△ABC的内角A,B,C的对边分别为a,b,c，已知sin⁡Csin⁡( A-B)=sin⁡Bsin⁡(C-A)．（1）证明：2a2=b2+c2；（2）若a=5,cos⁡A=25/31，求△ABC的周长．