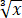高中数学-高考试题(上海市 2020年映射与函数)

填空题（2020年上海市）

已知 f(x) = x³, 则 f⁻¹(x) =______.

答案解析

讨论

高中数学

已知 z = 1 − 2i, 则 |z| =______.

(n+1)/(3n+2)=________.

已知 A = {1, 2, 4}, B = {2, 4, 5}, 则 A ∩ B =__________.

已知函数 f(x)=x3+klnx (k ∈ R) , f′(x) 为 f(x) 的导函数.(I) 当 k = 6 时,(i) 求曲线 y = f(x) 在点 (1, f(1)) 处的切线方程;(ii) 求函数 g(x)=f(x)+f'(x)+9/x 的单调区间和极值;(II) 当 k ⩾ −3 时, 求证: 对任意的 x1, x2 ∈ [1, +∞), 且 x1 > x2, 有f'(x1+x2)/2 > (f(x1 )-f(x2))/(x1-x2 ) .

已知 {an} 为等差数列, {bn} 为等比数列, a1 = b1 = 1, a5 = 5(a4 − a3), b5 = 4(b4 − b3).(I) 求 {an} 和 {bn} 的通项公式;(II) 记 {an} 的前 n 项和为 Sn, 求证: SnSn+2 < Sn+12 (n ∈ N∗);(III) 对任意的正整数 n, 设 cn = .求数列 {cn} 的前 2n 项和.

已知椭圆 x2/a2 +y2/b2 =1 (a > b > 0) 的一个顶点为 A(0, −3), 右焦点为 F , 且 |OA| = |OF|, 其中 O 为原点.(I) 求椭圆的方程;(II) 已知点 C 满足 3=, 点 B 在椭圆上 (B 异于椭圆的顶点), 直线 AB 与以 C 为圆心的圆相切于点P , 且 P 为线段 AB 的中点. 求直线 AB 的方程.

如图, 在三棱柱 ABC − A1B1C1 中, CC1⊥平面 ABC, AC ⊥ BC, AC = BC = 2, CC1 = 3, 点 D, E 分别在棱 AA1 和棱 CC1 上, 且 AD = 1, CE = 2, M 为棱 A1B1 的中点.(I) 求证: C1M ⊥ B1D;(II) 求二面角 B − B1E − D 的正弦值;(III) 求直线 AB 与平面 DB1E 所成角的正弦值.

在 △ABC 中, 角 A, B, C 所对的边分别为 a, b, c. 已知 a = 2√2, b = 5, c = .(I) 求角 C 的大小;(II) 求 sin A 的值;(III) 求 sin⁡(2A+π/4) 的值.

如图, 在四边形 ABCD 中, ∠B = 60º, AB = 3, BC = 6, 且 =λ, ·= -3/2, 则实数 λ 的值为_____, 若 M, N 是线段 BC 上的动点, 且 || = 1, 则· 的最小值为______.

已知 a > 0, b > 0, 且 ab = 1, 则 1/(2a)+1/(2b)+8/(a+b)的最小值为_______.

映射与函数

甲，乙两车分别从 A，B 两地同时出发相向而行，1 小时后，甲车到达 C 点，乙车到达 D点则能确定 AB 两地的距离【】(1)已知 C，D 两地距离(2) 已知甲，乙两车速度比

已知集合A={1,2,3}，映射f:A→A，且满足对任意x∈A，有f(f(x))≥x，且这样的f有________个.

设S={z∈C||z|=1}.求所有函数f:S→S，使得f为连续单射,且对任意z1,z2∈S，有f(z1 z2 )=f(z1)f(z2).

Find all functions f from the integers to the integers such that for all integers n：2f(f(n))=5f(n)-2n【译】求所有函数f:z→z，使得对任意整数n有：2f(f(n))=5f(n)-2n

函数 f(x) = 1/(x+1)+lnx 的定义域是__________.

用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量1/2，用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上,设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).( I )试规定f(0)的值,并解释其实际意义.(Ⅱ)试根据假定写出函数f(x)应该满足的条件和具有的性质.(Ⅲ)设f(x)=1/(1+x2 ).现有a(a>0)单位量的水，可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.

已知一企业一年营业额1.1亿元，每年增加0.05亿元，利润0.16亿元，每年增长4%.(1)求营业额前20季度的和.(2)请问哪年哪季度营业额是利润的18%？

已知x1,x2∈R，若对任意的x2-x1∈S,f(x2 )-f(x1)∈S，则有定义：f(x)是S关联的.(1)判断和证明f(x)=2x-1是否在[0,+∞)关联？是否有[0,1]关联?(2)若f(x)是在{3}关联的，在x∈[0,3)时f(x)=x2-2x，求解不等式：2≤f(x)≤3.(3)证明：f(x)是{1}关联的，且是在[0,+∞)关联的，当且仅当“f(x)在[1,2]是关联的”.

已知a∈R，函数f(x)=，若f[f(√6)]=3，则a=__________.

求函数y=的定义域，并在数轴上表示出来.

函数

设x²+ax+b=0之二根的差与x²+px+q=0之二根的差相等，求a,b,p,q之关系.

问下列联立方程，除x=y=z=0外，是否有其它解存在？如有，将解求出：

解方程组，并详细讨论之.

方程(x5-5x+k)=0有______个实根.

若f(x)=x5+px+q有有理根，且正整数p,q不大于100，则满足条件的(p,q)共有几组.

求19x+93y=4xy的整数解的组数.

已知函数 f(x) =.若函数 g(x) = f(x) − |kx2 − 2x| (k ∈ R) 恰有 4 个零点, 则 k 的取值范围是【】.

某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?

设a∈R，函数f(x)=，若f(x)在区间(0,+∞)内恰好有6个零点，则a的取值范围是【】

已知2lgx+lg2=lg⁡(x+6)，求x.