已知函数f(x)=x+1，若f(x)=a0/2+
ancosnx,x∈[0,π]，则
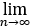n²sina2n-1 =______.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
填空题（2024年理工数学Ⅰ）
答案解析
-1/π（解答过程见word版）
讨论
设函数f(u,v)具有2阶连续偏导数，且df|(1,1)=3du+4dv，令y=f(cosx,1+x²)，则d²y/dx²|x=0=______.
若((1+ax²)sinx-1)/x³=6，则a=______.
设随机变量X,Y相互独立，且均服从参数为λ的指数分布，令Z=|X-Y|，则下列随机变量与Z同分布的是【 】
设随机变量X的概率密度为f(x)=，在X=x(0<x<1)的条件下，随机变量Y服从区间(x,1)上的均匀分布，则Cov(X,Y)=【 】
设随机变量X,Y相互独立，且X服从正态分布N(0,2),Y服从正态分布N(-2,2)，若P{2X+Y<a}=P{X>Y}，则a=【 】
设A是秩为2的3阶矩阵，α是满足Aα=0的非零向量，若对满足βTα=0的3维向量β均有Aβ=β，则【 】
设向量α1=,α2=,α3=，若α1,α2,α3线性相关，且其中任意两个向量均线性无关，则【 】
函数f(z)=1/(z-1)(z-2)在圆环区域：(1) 0<|z|<1；(2) 1<|z|<2；(3) 2<|z|<+∞；内是处处解析的。试把f(z)在这些区域内展成洛朗级数。
将函数f(x)=arctan(1+x)/(1-x)展开为x的幂级数.
将函数f(x)=1/4 ln(1+x)/(1-x)+1/2 arctanx-x展开成x的幂级数.
设a1,a2,⋯,an是n个实数，都落在区间(-1,1)里.(1)证明 ∏1≤i,j≤n(1+aiaj)/(1-aiaj )≥1(2)找出以上不等式中等号成立的充分必要条件.
设函数f(x)在区间(-1,1)内有定义，且f(x)=0，则【 】
设函数f(x,y)在点(0,0)处可微，f(0,0)=0,n= (∂f/∂x,∂f/∂y,-1)|(0,0)，非零向量r与n垂直，则【 】
设数列{an}满足a1=1,(n+1) an+1=(n+1/2) an，证明：当|x|<1时，幂级数an xn 收敛，并求其和函数.
证明：当x>0时，ln√x=1/(2n-1) ((x-1)/(1+x))2n-1 ，并讨论1/(2n-1) ((x-1)/(1+x))2n-1关于x∈(0,+∞)是否一致收敛.
设f(x)=,S(x)=a0/2+ancosnπx,-∞<x<+∞，其中an=2f(x)cosnπxdx (n=0,1,2,…)，则S(-5/2)等于【 】
已知a1=2,an+1=1/2 (an+1/an )，证明：(1)数列{an }收敛；(2) (an/an+1 -1) 收敛.