已知幂级数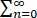 anxn的和函数为ln(2+x),则
anxn的和函数为ln(2+x),则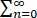 na2n =【 】
na2n =【 】
A、-1/6
B、-1/3
C、1/6
D、1/3
已知幂级数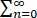 anxn的和函数为ln(2+x),则
anxn的和函数为ln(2+x),则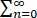 na2n =【 】
na2n =【 】
A、-1/6
B、-1/3
C、1/6
D、1/3
A
【解析】
解答过程见word版
设t>0,平面有界区域D由曲线y=√x ex与直线x=t,x=2t及x轴围成,D绕x轴旋转一周所成旋转体的体积为V(t),求V(t)的最大值.
设y(x)为微分方程x²y''+xy'-9y=0满足条件 y|x=1=2, y'|x=1=6的解.(1)利用变换x=et将上述方程化为常系数线性方程,并求y(x);(2)计算y(x)dx.
设平面有界区域D位于第一象限,由曲线xy=1/3,xy=3与直线y=1/3 x,y=3x围成,计算∬D(1+x-y)dxdy.
设向量α1=,α2=,α3=,若α1,α2,α3线性相关,且其中任意两个向量均线性无关,则ab=__________.
某物体以速度v(t)=t+ksinπt做直线运动,若它从t=0到t=3的时间段内平均速度是5/2,则k=__________.
设数列{an}满足a1=1,(n+1) an+1=(n+1/2) an,证明:当|x|<1时,幂级数an xn 收敛,并求其和函数.
幂级数n/(2n+(-3)n) x2n-1的收敛半径R=________.
已知幂级数(-1)nn(n+1) xn .(1)求幂级数的收敛半径、收敛区间以及和函数;(2)计算(-1)nn(n+1)/4n .
求幂级数(3+(-1)n)n/n xn的收敛半径,并判断它在收敛区间端点的收敛情况.
证明:(1)级数 sin(2nπx)/2n 在区间(-∞,+∞)上连续;(2)函数f(x)=sin(2nπx)/2n 在任何区间上不能逐次求导.
证明:当x>0时,ln√x=1/(2n-1) ((x-1)/(1+x))2n-1 ,并讨论1/(2n-1) ((x-1)/(1+x))2n-1关于x∈(0,+∞)是否一致收敛.
已知函数f(x)=x+1,若f(x)=a0/2+ancosnx,x∈[0,π],则n²sina2n-1 =______.
设a1=2,an+1=1/2(an+1/an )(n=1,2,…),证明:(1) an 存在;(2)级数(an/an+1 -1)收敛.
设正向数列{an}单调减少,且(-1)nan 发散,试问级数(1/(an+1))n 是否收敛?并说明理由.
设f(x)=,S(x)=a0/2+ancosnπx,-∞<x<+∞,其中an=2f(x)cosnπxdx (n=0,1,2,…),则S(-5/2)等于【 】
已知a1=2,an+1=1/2 (an+1/an ),证明:(1)数列{an }收敛;(2) (an/an+1 -1) 收敛.