设a1=2,an+1=1/2(an+1/an )(n=1,2,…),证明:
(1) 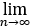 an 存在;
an 存在;
(2)级数 (an/an+1 -1)收敛.
(an/an+1 -1)收敛.
设a1=2,an+1=1/2(an+1/an )(n=1,2,…),证明:
(1) 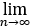 an 存在;
an 存在;
(2)级数 (an/an+1 -1)收敛.
(an/an+1 -1)收敛.
(1)显然an≥0(n=1,2,3,…),由于an+1-an=1/2 (an+1/an )-an=(1-an2)/(2an ),而an+1=1/2 (an+1/an )≥=1,于是an+1-an≤0,故数列{an}单调减少且有下界,所以an 存在.(2)由于数列{an}单调减少,所以有...
查看完整答案设f(x)连续,φ(x)=f(xt)dt,且f(x)/x=A(A为常数),求φ'(x)并讨论φ'(x)在x=0处的连续性.
设函数f(u)具有二阶连续导数,而z=f(exsiny)满足方程∂2z/∂x2+∂2z/∂y2=e2x z,求f(u).
设直线l:在平面π上,且平面π与曲面z=x2+y2相切于点(1,-2,5),求a,b的值.
计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz,其中C是曲线从z轴正向往z轴负向看,C的方向是顺时针的.
计算I=∭Ω(x2+y2)dV,其中Ω为平面曲线绕z轴旋转一周形成的曲面与平面z=8所围成的区域.
设两个相互独立的随机变量X和Y的方差分别为4和2,则随机变量3X-2Y的方差是【 】
设α1=,α2=,α3=,则三条直线a1 x+b1 y+c1=0,a2 x+b2 y+c2=0,a3 x+b3 y+c3=0,(其中ai2+bi2≠0,i=1,2,3)相交于一点的充要条件是【 】
设在区间[a,b]上f(x)>0,f' (x)<0,f''(x)>0,记S1=f(x)dx,S2=f(b)(b-a),S3=1/2[f(a)+f(b)](b-a),则【 】