设f(x)连续,φ(x)=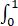 f(xt)dt,且
f(xt)dt,且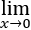 f(x)/x=A(A为常数),求φ'(x)并讨论φ'(x)在x=0处的连续性.
f(x)/x=A(A为常数),求φ'(x)并讨论φ'(x)在x=0处的连续性.
问答题(1997年理工数学Ⅰ)
答案解析
由题设f(x)/x=A知,f(0)=0,f'(0)=A,且有φ(0)=0.又φ(x)=f(xt) dt,令u=xt,则有φ(x)=(f(u)du)/x(x≠0),于是φ'(x)=(xf(x)-f(u)du)/x2 (x≠0).由导数的...
查看完整答案设f(x)连续,φ(x)=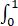 f(xt)dt,且
f(xt)dt,且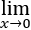 f(x)/x=A(A为常数),求φ'(x)并讨论φ'(x)在x=0处的连续性.
f(x)/x=A(A为常数),求φ'(x)并讨论φ'(x)在x=0处的连续性.
由题设f(x)/x=A知,f(0)=0,f'(0)=A,且有φ(0)=0.又φ(x)=f(xt) dt,令u=xt,则有φ(x)=(f(u)du)/x(x≠0),于是φ'(x)=(xf(x)-f(u)du)/x2 (x≠0).由导数的...
查看完整答案