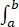大学数学-考研试题(理工数学Ⅱ 1987年定积分的概念与性质)

填空题（1987年理工数学Ⅱ）

f'(2x)dx=__________.

答案解析

1/2[f(2b)-f(2a)]

讨论

大学数学

∫f'(x)dx=__________.

((n-2)/(n+1))n=________.

积分中值定理的条件是__________，结论是____________.

曲线y=arctanx在横坐标为1的点处的切线方程是__________；法线方程是____________.

设y=ln⁡(1+ax)，其中a是非零常数，则y'=__________，y''=__________.

将函数f(x)=arctan⁡(1+x)/(1-x)展开为x的幂级数.

计算三重积分∭Ω(x+z)dV，其中Ω是由曲面z=与z=所围成的区域.

设曲线积分∫Cxy2dx+yφ(x)dy与路径无关，其中φ(x)具有连续的导数，且φ(0)=0，计算xy2dx+yφ(x)dy的值.

设z=f(2x-y)+g(x,xy)，其中函数f(t)二阶可导，g(u,v)具有连续的二阶偏导数，求∂2z/∂x∂y.

设A是n阶矩阵，且A的行列式|A|=0，则A中【】

定积分

f(x)在[0,1]上有连续导数，f(x)无零点，且f(0)=1,f(1)=2，则dx= __________。

利用δ函数计算下列积分(x2+1)δ(x2-2x-8)dx.

若f(x)为已知连续函数，I=tf(tx)dx，其中t>0,s>0，则I的值【】

设f(x)是连续函数，且f(x)=x+2f(t)dt=________.

证明：sin⁡(x²)dx>0.

求定积分x(sinx)arctan⁡(e-x)/(1+cos2⁡x )dx

证明：xasinxdx∙a-cosx dx≥π³/4其中，a>0为常数.

设f(a)=0,f(x)在[a,b]上的导数连续，求证：1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] ⁡|f'(x)|,x∈[a,b]

|x|dx = ______.

定积分的概念与性质

当某公司推出一个新的社交软件时，公司的市场部门除了会关心该软件的活跃客的总人数随时间的变化，也会对客户群体的一些特征做具体的调研和分析。我们用n(t,x)表示客户的数量密度(以下简称密度)，这里t表示时间，而x表示客户对该社交软件的使用时长，那么在t时刻，对于0<x1<x2，使用时长介于x1和x2之间的客户数量为n(t,x)dx。我们假设，密度n(t,x)随着时间演化受以下几个因素的影响：假设1.当客户持续使用该社交软件时,他的使用时长随时间线性增长。假设2.客户在使用过程中，可能会停止使用，我们假设停止速率d(x)>0只跟使用时长x有关。假设3.新客户的来源有两个。①公司的宣传：单位时间内因此增加的人数是时间的函数，用c(t)表示。②老客户的宣传：老客户会主动向自己的同事、朋友等推荐使用该社交软件，推荐成功的速率跟客户的使用时长x有关，记作b(x)。假设如果在某一时刻，记为t=0时，密度函数是已知的，n(0,x)=n0 (x)。可以推导出，n(t,x)的时间演化满足如下的方程 (1)这里N(t)可解读为新客户的增加速率。我们假设b,d∈(0,∞)，即b(x)和d(x)正且(本质)有界。以下,我们先做一个简化假设：c(t)≡0，即新客户的增加只跟老客户的宣传有关。(i)问答题(10分)根据假设1和假设2，形式地推导出(1)中n(t,x)所满足的偏微分方程，需要在推导过程中指出模型假设和数学表达式之间的对应关系。再根据假设3，解释(1)中N(t)的定义的含义。(ii)问答题(10分)我们想要研究新客户的增加速率N(t)和推荐成功速率b(x)之间的关系。为此,请推导出一个N(t)所满足的方程，且方程中只包含N(t),n0 (x),b(x),d(x)，而不包含n(t,x)。并证明，N(t)满足如下估计|N(t)|≤‖b‖∞|n0 (x)|dx,这里‖∙‖∞表示L∞范数。(iii)证明题(10分)最后，我们想要研究，在充分长的时间之后，数量密度函数n(t,x)有什么渐近的趋势。由于客户总人数可能一直在增加，所以我们不方便直接研究数量密度函数n(t,x)，而更应该去看一个重整化的密度函数。为此，我们首先假设如下的特征值问题有唯一解(λ0,φ(x))：并且它的对偶问题也有唯一的解ψ(x)：然后，我们定义重整化密度n ̃(t,x)≔n(t,x)e-λ0 t。证明，对于任意凸函数H:R+→R+满足H(0)=0，我们有d/dt ψ(x)φ(x)H()dx≤0,∀t≥0,并证明ψ(x)n(t,x))dx=eλ0t ψ(x) n0 (x)dx.

数值求积f(x)dx时(1)试写出直接用梯形公式的计算式T1；(2)将[a,b]n等分，用Tn表示用复化梯形公式求得的积分值，试写出Tn的计算式；(3)若将步长分半（即步长二分），试给出T2n与Tn的递推关系；(4)若用精度控制|T2n - Tn |<ε，试写出“变步长梯形法”的算法框图.

用Romberge方法求dx的近似值。（给定n=4）

设f(x)在[0,1]上连续，f(x)dx=0,xf(x)dx=1，则存在x0∈[0,1]使|f(x0 )|>4.

设f(x)连续，且f(t)dt=x，则f(7)=______.

设f(x),g(x)在区间[a,b]上连续，且g(x)取正值，由积分中值定理有f(t)g(t)dt=f(ξ)g(t) dt(a≤ξ≤x≤b)若f+' (a)存在且f+' (a)≠0，求(ξ-a)/(x-a).

设f(x)在(0,1)可微，且有x2 f(x) dx=0，证明：存在θ∈(0,1)，使得f' (θ)=-f(θ)/θ.

设连续函数f(x)满足f(a+b-x)=f(x),∀x∈[a,b]，则积分xf(x)dx等于【】

设f∈[0,2π]，证明：f(x)|sinnx|dx=2/πf(x)dx.

d/dx xcost2dt=______________.