积分中值定理的条件是__________,结论是____________.
曲线y=arctanx在横坐标为1的点处的切线方程是__________;法线方程是____________.
设y=ln(1+ax),其中a是非零常数,则y'=__________,y''=__________.
将函数f(x)=arctan(1+x)/(1-x)展开为x的幂级数.
计算三重积分∭Ω(x+z)dV,其中Ω是由曲面z=与z=所围成的区域.
设曲线积分∫Cxy2dx+yφ(x)dy与路径无关,其中φ(x)具有连续的导数,且φ(0)=0,计算xy2dx+yφ(x)dy的值.
设z=f(2x-y)+g(x,xy),其中函数f(t)二阶可导,g(u,v)具有连续的二阶偏导数,求∂2z/∂x∂y.
设函数f(x)=x2,0≤x<1,而S(x)=bnsinnπx,-∞<x<+∞,其中bn=2f(x)sinnπxdx,x=1,2,3,…,则S(-1/2)等于【 】
设线性无关的函数y1,y2,y3都是二阶非齐次线性方程y''+p(x) y'+q(x)y=f(x)的解,C1,C2是任意常数,则该非齐次方程的通解是【 】
设f(x)在[0,1]上连续,f(x)dx=0,xf(x)dx=1,则存在x0∈[0,1]使|f(x0 )|>4.
设f(x)连续,且f(t)dt=x,则f(7)=______.
设f(x)是连续函数,且f(x)=x+2f(t)dt=________.
证明:xasinxdx∙a-cosx dx≥π³/4其中,a>0为常数.
设f(a)=0,f(x)在[a,b]上的导数连续,求证:1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] |f'(x)|,x∈[a,b]
设f(x)在(0,1)可微,且有x2 f(x) dx=0,证明:存在θ∈(0,1),使得f' (θ)=-f(θ)/θ.
设I1=x/2(1+cosx) dx,I2=ln(1+x)/(1+cosx) dx,I3=2x/(1+sinx) dx,则【 】


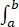 f(x)dx=f(ξ)(b-a).
f(x)dx=f(ξ)(b-a).