计算三重积分∭Ω(x+z)dV,其中Ω是由曲面z=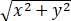 与z=
与z=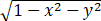 所围成的区域.
所围成的区域.
计算题(1989年理工数学Ⅰ)
答案解析
∭Ω(x+z)dV=∭ΩxdV+∭ΩzdV.由于Ω关于xOy平面对称,被积函数x是奇函数,故∭ΩxdV=0.∭ΩzdV=dθdφρcosφ∙ρ2sinφdρ=2π∙1/2 sin2φ∙1/4=π/...
查看完整答案讨论
设曲线积分∫Cxy2dx+yφ(x)dy与路径无关,其中φ(x)具有连续的导数,且φ(0)=0,计算xy2dx+yφ(x)dy的值.
设z=f(2x-y)+g(x,xy),其中函数f(t)二阶可导,g(u,v)具有连续的二阶偏导数,求∂2z/∂x∂y.
设函数f(x)=x2,0≤x<1,而S(x)=bnsinnπx,-∞<x<+∞,其中bn=2f(x)sinnπxdx,x=1,2,3,…,则S(-1/2)等于【 】
设线性无关的函数y1,y2,y3都是二阶非齐次线性方程y''+p(x) y'+q(x)y=f(x)的解,C1,C2是任意常数,则该非齐次方程的通解是【 】
已知曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0,则点P的坐标是【 】
随机变量ξ在(1,6)上服从均匀分布,则方程x2+ξx+1=0有实根的概率是______.
甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为______.
已知随机事件A的概率P(A)=0.5,随机事件B的概率P(B)=0.6以及条件概率P(B|A)=0.8,则和事件A∪B的概率P(A∪B)=______.
计算二重积分:∬Dds其中,积分区域D为曲线y(x)=与直线y=0所围成的区域.提示:①首先考察曲线y=y(x)⟹F(x,y)=0为何种曲线,②然后采用“平面极坐标”方法作计算?
计算二重积分∬D3x/(x2+xy3 ) dxdy,D:平面曲线xy=1,xy=3,y2=x,y2=3x所围成的有界闭区域.
设空间区域Ω1:x2+y2+z2≤R2,z≥0,Ω2:x2+y2+z2≤R2,x≥0,y≥0,z≥0,则【 】
已知函数f(t)=dxsin(x/y)dy,则f'(π/2)=______.
求(x2+y2+z2 )2=4(x2+y2-z2)所围立体的体积.
求三重积分∭Ω(x2+y2)dxdydz,其中积分区域Ω为x2+y2=2z与z=1围成的区域.
已知V是三个坐标平面以及x+y+2z=1,x+y+2z=2围成的封闭区域,求∭V1/(x+y+2z)2 dV
已知u是Ω=[0,1]×[0,1]×[0,1]上的正值连续函数,Ip(u)=(∭Ωupdxdydz)1/p证明:Ip(u)=
求∭Ω(x2+y2+z)dV,其中Ω是由曲线绕z轴旋转一周而成的曲面与平面z=4所围成的立体.
设S为椭球面x2/2+y2/2+z2=1的上半部分,点P(x,y,z)∈S,π为S在P处的切平面,ρ(x,y,z)为点O(0,0,0)到平面π的距离,求∬Sz/(ρ(x,y,z)) dS.
设A,B,C满足:A,B互不相容,A,C互不相容,B,C相互独立,P(A)=P(B)=P(C)=1/3,则P[(B∪C)│(A∪B∪C) ]=__________.
若微分方程y''+ay'+by=0的解在(-∞,+∞)上有界,则【 】
已知向量α1=,α2=,α3=,β=,γ=k1 α1+k2 α2+k3 α3,若γTαi=βTαi (i=1,2,3),则k12+k22+k32=______.
二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【 】

