设空间区域Ω1:x2+y2+z2≤R2,z≥0,Ω2:x2+y2+z2≤R2,x≥0,y≥0,z≥0,则【 】
A、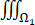 xdV=4
xdV=4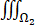 xdV
xdV
B、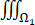 ydV=4
ydV=4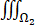 ydV
ydV
C、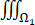 zdV=4
zdV=4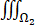 zdV
zdV
D、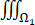 xyzdV=4
xyzdV=4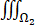 xyzdV
xyzdV
设空间区域Ω1:x2+y2+z2≤R2,z≥0,Ω2:x2+y2+z2≤R2,x≥0,y≥0,z≥0,则【 】
A、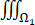 xdV=4
xdV=4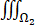 xdV
xdV
B、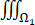 ydV=4
ydV=4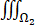 ydV
ydV
C、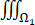 zdV=4
zdV=4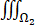 zdV
zdV
D、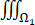 xyzdV=4
xyzdV=4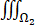 xyzdV
xyzdV
C
设y=f(x)是方程y''-2y'+4y=0的一个解,且f(x0)>0,f' (x0)=0,则函数f(x)在点x0处【 】
若函数y=f(x)可导,且f'(x0)=1/2,则当∆x→0时,该函数在x=x0处的微分dy是【 】
设4阶矩阵A=(α,γ2,γ3,γ4 ),B=(β,γ2,γ3,γ4),其中α,β,γ2,γ3,γ4均为四维列向量,且已知行列式|A|=4,|B|=1,则行列式|A+B|=________.
设f(x)连续,且f(t)dt=x,则f(7)=______.
设f(x)是周期为2的周期函数,它在区间(-1,1]上定义为f(x)=,则f(x)的傅里叶级数在x=1处收敛于______.
设f(t)=t(1+1/x)2tx ,则f' (t)=__________.
设随机变量X,Y相互独立,其概率密度函数分别为:fX (x)=,fY(y)= 求Z=2X+Y的概率密度函数.
已知连续随机变量X的概率密度函数为f(x)=,则X的数学期望为______;X的方差为______.
设在一次试验中,事件A发生的概率为p,现进行n次独立试验,则A至少发生一次的概率为__________;而事件A至多发生一次的概率为__________.
计算二重积分:∬Dds其中,积分区域D为曲线y(x)=与直线y=0所围成的区域.提示:①首先考察曲线y=y(x)⟹F(x,y)=0为何种曲线,②然后采用“平面极坐标”方法作计算?
计算二重积分∬D3x/(x2+xy3 ) dxdy,D:平面曲线xy=1,xy=3,y2=x,y2=3x所围成的有界闭区域.
已知函数f(t)=dxsin(x/y)dy,则f'(π/2)=______.
计算∬Ωe(x-y)/(x+y) dΩ,其中Ω:x≥0,y≥0,x+y≤1.
求(x2+y2+z2 )2=4(x2+y2-z2)所围立体的体积.
求三重积分∭Ω(x2+y2)dxdydz,其中积分区域Ω为x2+y2=2z与z=1围成的区域.
已知V是三个坐标平面以及x+y+2z=1,x+y+2z=2围成的封闭区域,求∭V1/(x+y+2z)2 dV
已知u是Ω=[0,1]×[0,1]×[0,1]上的正值连续函数,Ip(u)=(∭Ωupdxdydz)1/p证明:Ip(u)=
求∭Ω(x2+y2+z)dV,其中Ω是由曲线绕z轴旋转一周而成的曲面与平面z=4所围成的立体.
计算三重积分∭Ω(x+z)dV,其中Ω是由曲面z=与z=所围成的区域.
与两直线及(x+1)/1=(y+2)/2=(z-1)/1都平行且过原点的平面方程为______________.
已知三维向量空间的基底为α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T,则向量β=(2,0,0)T在此基底下的坐标是____________.
设(f(x)-f(a))/(x-a)2=-1,则在x=a处【 】
求正的常数a与b,使等式1/(bx-sinx)t2/dt=1成立.
计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面,其法向量与y轴正向的夹角恒大于π/2.