大学数学-考研试题(理工数学Ⅰ 1987年平面及其方程)

填空题（1987年理工数学Ⅰ）

与两直线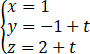及(x+1)/1=(y+2)/2=(z-1)/1都平行且过原点的平面方程为______________.

答案解析

x-y+z=0

讨论

大学数学

由曲线y=lnx与两条直线y=e+1-x及y=0所围成的平面图形的面积是______.

当x=______时，函数y=x∙2x取得极小值.

求定解问题对应的贝塞尔方程

写出定解问题的解的表示 ,S:x2+y2+x2=1.

求边值问题的固有值和固有函数

求方程uxx+6uxy-7uyy=0的通解。

设有一根具有绝热的侧表面的均匀细杆，它的初始温度为φ(x)，在一端有热流密度q1进入，另一端与温度为θ(t)的介质有热交换。写出定解问题。

试将函数f(z)=1/(1+z2 )在区域1<|z|<+∞中展开为罗朗级数。

试将函数f(z)=1/(1+z2 )在区域2<|z-i|<+∞中展开为罗朗级数。

试将函数f(z)=1/(1+z2 )在区域0<|z-i|<2中展开为罗朗级数。

向量代数与解析几何

面条是中华传统美食，花样不断翻新。清晨，擀宽面的张师傅别出心裁，把他的宽面条两头粘上，变成了宽面圈儿，如图：他平时切面条一样，把宽面圈儿沿着中心线切开，就得到两个完全同样的宽面圈儿，如图：张师傅灵机一动，重新将面条拧了一下，再两头粘上。这样竟然成了数学中常常讲到的莫比乌斯带（以德国数学家奥古斯特●莫比乌斯命名），如图：接着，他灵机两动，三动，直至n动。将宽面拧了两个，三下，直至n下，总以如图的右手内旋的方式来拧，然后照样地两头粘上。这些宽面圈儿在数学上还没有固定的名称。张师傅把莫比乌斯带称作1旋圈面，拧两下、三下的称作2旋、3旋圈面，总之，拧n下就是旋圈面；n为2、3、7的情形如图：起先没有拧就粘上的，普普通通，只称作平凡圈面，或者0旋圈面。在线师傅看来，不同旋数的圈面是彼此不同的（因为只在厨房里摆放来，摆放去，总不能把一种变成另一种）。张师傅把他的多旋圈面开店上架，一时网红。有人为百岁老人订制100旋圈面，有人为公司年会订制2019旋圈面，（张师傅拧得手都酸了）。试问：张师傅要是依旧沿中心线切开这两种圈面，分别会得到什么？【】

2019年第一届阿里巴巴数学竞赛的优胜者们在参加集训营的时候，集体送给主办方负责人的礼物，是一个有60个全等的三角形面的多面体。从图中我们可以看到，这个多面体的表面是60个全等的空间四边形拼接而成的。一个空间n边形是指由一个平面n边形沿若干条对角线做适当翻折（即在选定的对角线处形成适当的二面角)后得到的空间图形。两个空间图形全等指的是它们可以通过R3中的一个等距变换完全重合。一个多面体指的是一个空间有界区域，其边界可以由有限多个平面多边形沿公共边拼接而成。1. 判断题(4分) 我们知道2021=43×47.那么是否存在一个多面体，它的表面可以由43个全等的空间47边形拼接而成?2. 问答题(6分) 请对你的判断给出逻辑的解释。

已知α=(1,2,3);β=(1,1/2,1/3)，设A=αTβ，则An=__________。

已知曲线C:，求C上的点到xoy坐标面距离的最大值.

曲面z=x+2y+ln⁡(1+x2+y2)在(0,0,0)处的切平面方程为__________.

设矩阵是满秩的，则直线(x-a3)/(a1-a2 )=(y-b3)/(b1-b2 )=(z-c3)/(c1-c2 )与直线(x-a1)/(a2-a3 )=(y-b1)/(b2-b3 )=(z-c1)/(c2-c3 )【】

设空间直角坐标系中的四点A(1,1,1),B(1,2,3),C(1,2,4),D(2,3,4),则点A到平面BCD的距离d=__________.

已知点A与B的直角坐标分别为(1,0,0)与(0,1,1).线段AB绕z轴旋转一周所成的旋转曲面为S.求由S及两平面z=0,z=1所围成的立体体积.

设(a×b)∙c=2，则[(a+b)×(b+c)]∙(c+a)=________.

设一平面经过原点及点P(6,-3,2)，且与平面4x-y+2z=8垂直，则此平面方程为______________.

平面及其方程

过点M(1,2,-1)且与直线垂直的平面方程是__________.

已知两条直线的方程是 l1:(x-1)/1=(y-2)/0=(z-3)/(-1);l2:(x+2)/2=(y-1)/1=z/1.则过l1且平行于l2的平面方程是____________.

确定常数λ，使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度，并求u(x,y).

从船上向海中沉放某种探测仪器，按探测要求，需确定仪器的下沉深度y(从海平面算起)与下沉速度v之间的函数关系.设仪器在重力作用下，从海平面由静止开始铅直下沉，在下沉过程中还受到阻力和浮力的作用.设仪器的质量为m，体积为B，海水比重为ρ，仪器所受的阻力与下沉速度成正比，比例系数为k(k>0).试建立y与v所满足的微分方程，并求出函数关系式 y= y(v).

计算曲面积分I=∬Σ (axdydz+(z+a)2dxdy)/(x2+y2+z2 )1/2 ，其中Σ为下半球面z=-的上侧，a为大于零的常数.

已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T，试写出线性方程组(II)有通解，并说明理由.

设f(x)=其中g(x)是有界函数，则f(x)在x=0处【】

设y=y(x),z=z(x)是由方程z=xf(x+y)和F(x,y,z)=0所确定的函数，其中f和F分别具有一阶连续导数和一阶连续偏导数，求dz/dx.

设函数y(x)(x≥0)二阶可导，且y' (x)>0,y(0)=1.过曲线y=y(x)上任意一点P(x,y)作该曲线的切线及x轴的垂线，上述两直线与x轴所围成的三角形的面积记为S1，区间[0,x]上以y=y(x)为曲边的曲边梯形面积记为S2，并设2S1-S2恒为1，求此曲线y=y(x)的方程.

设S为椭球面x2/2+y2/2+z2=1的上半部分，点P(x,y,z)∈S,π为S在P处的切平面，ρ(x,y,z)为点O(0,0,0)到平面π的距离，求∬Sz/(ρ(x,y,z)) dS.