求定解问题对应的贝塞尔方程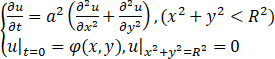
计算题(2004年秋电子科技大学)
答案解析
令u(x,y,t)=V(x,y)T(t)得T' (t)=a2 λT(t)=0 ∂2 V/∂x2 +∂2 V/∂y2+λV=0 Θ'' (θ)+μΘ(θ)=0 ρ2 P'' (ρ)+ρP' (ρ)+(λ...
查看完整答案求定解问题对应的贝塞尔方程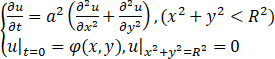
令u(x,y,t)=V(x,y)T(t)得T' (t)=a2 λT(t)=0 ∂2 V/∂x2 +∂2 V/∂y2+λV=0 Θ'' (θ)+μΘ(θ)=0 ρ2 P'' (ρ)+ρP' (ρ)+(λ...
查看完整答案