求解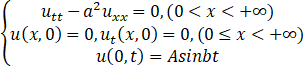
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（2004年春电子科技大学）
答案解析
u(x,t)=f1 (x+at)+f2 (x-a)f1 (x)+f2 (x)=0,f1' (x) f2'(x)=0 所以, f1 (x)=-f2 (x)=c,x≥0f1 (at)+f2 (-at)=c...
查看完整答案讨论
若函数w=f(z)在某个区域D内是解析的，且f' (z)=0，试证f(z)是一个常量。
若函数w=f(z)在某个区域D内是解析的，且在D内是解析的，试证f(z)是一个常量。
若函数w=f(z)在某个区域D内是解析的，且|f(z)|在D内是一个常量，试证f(z)是一个常量。
若函数w=f(z)在某个区域D内是解析的，且 Ref(z)在D内是一个常量，试证f(z)是一个常量。
计算积分I=∫c(ez dz)/(z2+1)2 ,其中积分路线c为椭圆：4x2+y2-2y-8=0正向一周。
试将函数f(z)=1/(1+z2 )在区域0<|z-i|<2中展开为罗朗级数。
试将函数f(z)=1/(1+z2 )在区域2<|z-i|<+∞中展开为罗朗级数。
差分方程△yt = t的通解为____________________.
设物体A从点(0,1)出发，以速度大小为常数v沿y轴正向运动，物体B从点(-1,0)与A同时出发，其速度大小为2v，方向始终指向A，试建立物体B的运动轨迹所满足的微分方程，并写出初始条件.
若连续函数f(x)满足关系式f(x)=f(t/2)dt+ln2，则f(x)等于【 】
设u(x,y)=x2+xy-y2，求出解析函数f(z)=u(x,y)+iv(x,y).
设u(x,y)=ex(xsiny+ycosy)，求出解析函数f(z)=u(x,y)+iv(x,y).
设有一根具有绝热的侧表面的均匀细杆，它的初始温度为φ(x)，在一端有热流密度q1进入，另一端与温度为θ(t)的介质有热交换。写出定解问题。