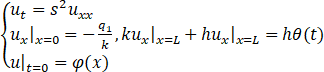设有一根具有绝热的侧表面的均匀细杆，它的初始温度为φ(x)，在一端有热流密度q1进入，另一端与温度为θ(t)的介质有热交换。写出定解问题。
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
试将函数f(z)=1/(1+z2 )在区域1<|z|<+∞中展开为罗朗级数。
试将函数f(z)=1/(1+z2 )在区域2<|z-i|<+∞中展开为罗朗级数。
试将函数f(z)=1/(1+z2 )在区域0<|z-i|<2中展开为罗朗级数。
计算积分I=∫c(ez dz)/(z2+1)2 ,其中积分路线c为椭圆：4x2+y2-2y-8=0正向一周。
设u(x,y)=ex(xsiny+ycosy)，求出解析函数f(z)=u(x,y)+iv(x,y).
设u(x,y)=x2+xy-y2，求出解析函数f(z)=u(x,y)+iv(x,y).
若函数w=f(z)在某个区域D内是解析的，且 Ref(z)在D内是一个常量，试证f(z)是一个常量。
若函数w=f(z)在某个区域D内是解析的，且|f(z)|在D内是一个常量，试证f(z)是一个常量。