-
关注“优题吧”，分配平台账号.
竞赛2024年阿里巴巴( )
几位同学假期组成一个小组去某市旅游. 该市有6座塔，它们的位置分別为A、B、C、D、E、F. 同学们自由行动一段时间后，每位同学都发现，自己在所在的位置只能看到位于A、B、C、D处的四座塔，而看不到位于E和F的塔，已知：
(1)同学们的位置和塔的位置均视为同一平面上的点，且这些点彼此不重合；
(2)A、B、C、D、E、F 中任意3点不共线；
(3)看不到塔的唯一可能就是视线被其它的塔所阻挡，例如，如果某位同学所在的位置P和A、B共线，且A在线段PB上，那么该同学就看不到位于B处的塔.
请问，这个旅游小组最多可能有多少名同学？
A、3
B、4
C、6
D、12
由于任意三座塔的位置不共线. 所以对任意一位同学来说. E和F处的塔必然是被两座不同的塔阻挡了视线.
任取前面的2座塔(不妨设为A处和B处的塔). 假设一位同学的视线是被这2座塔阻挡，那么该同学的位置或者是EA的延长线和FB的延长线的交点，或者是EB的延长线和FA 的延长线的交点.
然而，如果EA的延长线和FB的延长线有交点，那么AEFB是一个凸多边形，这意味着EB 和FA 的交点在这两条线段的内部. 因此，被A处和B处的塔阻挡住视线的同学最多有一位.
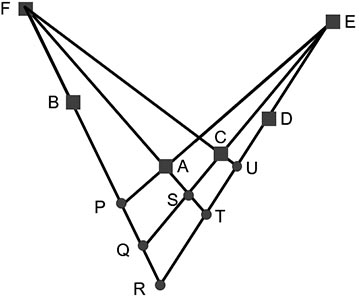
由于在前4座塔中选取2座塔的方式有6种，所以同学的数目不超过6，下图是一个取到6的例子(P、Q、R、S、T、U 是同学们的位置).
考博2004年秋电子科技大学( )
求定解问题对应的贝塞尔方程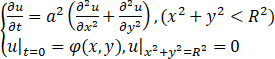
令u(x,y,t)=V(x,y)T(t)得
T' (t)=a2 λT(t)=0
∂2 V/∂x2 +∂2 V/∂y2+λV=0
Θ'' (θ)+μΘ(θ)=0
ρ2 P'' (ρ)+ρP' (ρ)+(λρ2-μ)P(ρ)=0
r2 F'' (r)+rF' (r)+(r2-n2 )F(r)=0.
考博2004年秋电子科技大学( )
写出定解问题的解的表示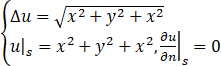 
,S:x2+y2+x2=1.
u=∬S[G(M,M0 ) ∂u/∂n-u(M) ∂G(M,M0 )/∂n] ds-∭VG(M,M0)f(M) dv
=∬S(x2+y2+z2 ) ∂G(M,M0 )/∂n ds-∭VG(M,M0)
dv.
G(M,M0 )=1/4π(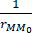
-1/r0 ),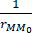
u(M0 )=1/4π [∬S(r2 (1-r02 ))/(1+r02-2r0 cosγ)^(3/2) ds-1/4π ∭Vr(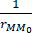 -1/r0 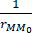) dv].
考博2004年秋电子科技大学( )
求边值问题的固有值和固有函数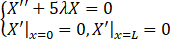
λ<0不可能
λ=0,X=a≠0
λ>0,λn=(n2π2)/(5L2 ),Xn=cos (nπx/L)(n=0,1,2,…).
考博2004年秋电子科技大学( )
求方程uxx+6uxy-7uyy=0的通解。
(y')2-6y'-7=0,(y'-7)(y'+1)=0
u=f(y-7x)+g(y+x).