求解理想不可压缩流体绕圆柱流动的速度势函数u(r,θ),满足
urr+1/r ur+1/r2 uθθ,r>a(半径为a的圆外区域),
ur (a,θ)=0,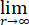 u=Vrcosθ,V为常数.
u=Vrcosθ,V为常数.
求解理想不可压缩流体绕圆柱流动的速度势函数u(r,θ),满足
urr+1/r ur+1/r2 uθθ,r>a(半径为a的圆外区域),
ur (a,θ)=0,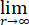 u=Vrcosθ,V为常数.
u=Vrcosθ,V为常数.
暂无答案
求解热传导方程定解问题。ut=uxx-2u 0<x<π,t>0,u(x,0)=sinx,u(0,t)=0,u(π,t)=0.
求解波动方程定解问题。4utt=25uxx -∞<x<+∞,t>0,u(x,0)=sin2x,ut (x,0)=0.
用数学归纳法证明:对于复n维空间Vn上任意多个两两可交换的线性变换所组成的集合S具有公共的特征向量.
设对角矩阵A的特征多项式为 φ(λ)=(λ-λi)ni (诸λi两两互异),求所有和A可交换的矩阵全体所组成的线性空间的维数.
设A=为n×n正定矩阵,证明:|A|≤a11 a22…ann.其中符号|∙|表示行列式.
设A=(aij)n×n为正定矩阵.证明:f(x1,x2,…,xn )=是负定二次型,其中符号|∙|表示行列式.
设A是n×n实对称矩阵,证明:存在一个实数k使得对任意一个实n维向量x都有|x' Ax|≤kx'x,其中x'表示向量x的转置.
设A,B,C,D都是n×n矩阵,且|A|≠0,AC=CA,证明=|AD-CB|.
设A是一个n×n实矩阵,秩(A)=1,证明A2=kA,其中k为一实数.
设α1,α2,…,αr是n维向量.令β1=α2+α3+⋯+αr,β2=α1+α3+⋯+αr,…,βr=α1+α2+⋯+αr-1.证明向量组β1,β2,…,βr与向量组α1,α2,…,αr有相同的秩.