大学数学-考博试题(北京大学 2005年正定矩阵)

证明题（2005年北京大学）

设A=(a_ij)_n×n为正定矩阵.证明：

f(x₁,x₂,…,x_n )=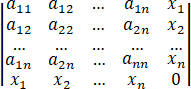

是负定二次型，其中符号|∙|表示行列式.

答案解析

暂无答案

讨论

正定矩阵

设A是n级实对称矩阵，证明rank(A)=n的充要条件是：存在实对称矩阵B使AB+B'A是正定矩阵。

设S1,S3为实对称矩阵，S2为实矩阵，则矩阵S=为正定矩阵的充要条件为矩阵S3与矩阵S1-S2 S3-1 S2'皆为正定矩阵。

设A为实对称矩阵。证明当实数t充分大之后，tI+A是正定矩阵，其中I表示单位矩阵。

设A是n阶正定矩阵，B为n阶实方阵，证明：(1)若B'=B,则AB的特征值为实数；(2)若B正定,则AB的特征值皆大于0；(3)若B正定,且AB=BA,则AB正定。

设A为正交阵，且A|=-1，证明：A+E不可逆.

设A是n阶正定矩阵，E是n阶单位矩阵，证明A+E的行列式大于1.

设A,B均为n阶实对称阵，A的特征值均小于a，B的特征值均小于b.证明：对任意的k>a+b,A+B-kE是负定矩阵.

设A=为n×n正定矩阵，证明：|A|≤a11 a22…ann.其中符号|∙|表示行列式.

设x1-x2=a1,x2-x3=a2,x3-x4=a3,x4-x5=a4,x5-x1=a5。证明此方程组有解的充分必要条件为ai =0。

北京大学齐次微分方程

正定二次型

给定方程x''+8x'+7x=f(t)，其中f(t)在(-∞,+∞)上连续。如果f(t)=0，则上述方程的每一个解当t→+∞时都趋于零。

求解微分方程组的初值问题

考虑方程x''+k2 x=f(t)，其中k为常数，函数f(t)于0≤t<+∞上连续。(1)当k≠0时求上述方程满足初始条件x(0)=1,x' (0)=-1的解。(2)证明当k=0时上述方程的通解可表示为x=c1+c2 t+(t-s)f(s)ds 其中c1,c2为任意常数。

证明微分方程初值问题：的解在α<t<β上存在且惟一，其中a(t),b(t)均在区间α<t<β上连续，α<x_0<β,x_0为任意实数。

北京大学齐次微分方程

给定偏微分方程：uxx+4uxy+3uyy=2.(1)判别方程的类型并求通解；(2)对该方程提定解条件：①u(x,x)=0,ux (x,x)=0或②u(0,y)=0,ux (0,y)=0问哪种定解条件下的定解问题是不适定的？为什么？(3)求出方程满足(2)中适定的定解条件的解。

利用积分变换方法求解定解问题，

利用积分变换方法求解定解问题，

利用Green函数法求定解问题，

设y=φ(x)满足微分不等式dy/dx+a(x)y≤0 其中函数a(x)在x≥0上连续，证明：φ(x)≤φ(0) ,(x≥0).

矩阵

设A=，则A-1=__________，A2022=__________，A的最大奇异值σ1=__________.

设=QR，其中Q是正交方阵，R是对角线元素大于0的上三角方阵，则R=________.

设A是2022阶可逆对称实方阵，则A必有2021阶非零主子式

设α1,…,αn和β1,…,βn是线性空间V的两组基，V上的线性变换A把每个αi映成βi,i=1,…,n.证明：A在α1,…,αn下的矩阵和在β1,…,βn下的矩阵相等.

设A,B为n阶可逆矩阵，E为n阶单位矩阵，M*为M的伴随矩阵，则=【】

设A,B为n阶实矩阵，下列结论不成立的是【】

已知A=(1) 求正交矩阵P，使得PTAP为对角矩阵；(2) 求正定矩阵C，使得C2 = (a+3)E-A.

已知矩阵A=，若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵，则P,Q可以分别取【】

若x=(-1,2,3,0,4)，求‖x‖1,‖x‖2,‖x‖∞.

设A=，求‖x‖1,‖x‖F,‖x‖∞.