大学数学-考研试题(理工数学Ⅱ 2023年分块矩阵)

单项选择（2023年理工数学Ⅱ）

设A,B为n阶可逆矩阵，E为n阶单位矩阵，M*为M的伴随矩阵，则=【】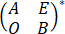

A、

B、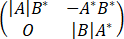

C、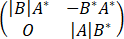

D、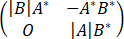

答案解析

D

讨论

大学数学

设函数f(x)=(x2+a) ex，若f(x)没有极值点，但曲线y=f(x)有拐点，则a的取值范围是【】

若函数f(a)=1/(x(lnx)a+1) dx在a=a0处取得最小值，则a0=【】

已知{xn },{yn}满足x1=yn=1/2,xn+1=sinxn,yn+1=yn2 (n=1,2,⋯) ，则当n→∞时【】

函数f(x)=的一个原函数为【】

设二维随机变量(X,Y)的概率密度为f(x,y)=(Ⅰ)求X与Y的方差；(Ⅱ)X与Y是否相互独立；(Ⅲ)求Z=X²+Y²的概率密度.

已知二次型f(x1,x2,x3 )=x12+2x22+2x32+2x1 x2-2x1 x3,g(y1,y2,y3 )=y12+y22+y32+2y2 y3.(Ⅰ)求可逆变换x=Py，将f(x1,x2,x3)化为g(y1,y2,y3);(Ⅱ)是否存在正交变换x=Qy，将f(x1,x2,x3)化为g(y1,y2,y3).

设函数f(x)在[-a,a]上具有二阶连续导数，证明：(Ⅰ)若f(x)=0，则存在ξ∈(-a,a)，使得f''(ξ)=1/a² [f(a)+f(-a)]；(Ⅱ)若f(x)在(-a,a)内取得极值，则存在η∈(-a,a)，使得|f''(η)|≥1/2a²|f(a)-f(-a)|.

设空间有界区域Ω中，柱面x²+y²=1与平面z=0和x+z=1围成，Σ为Ω边界的外侧，计算曲面积分I=∰Σ2xzdydz+xzcosydzdy+3yzsinxdxdy

求函数f(x,y)=(y-x²)(y-x³)的极值.

设曲线y=y(x)(x>0)经过点(1,2)，该曲线上任一点P(x,y)到y轴的距离等于该点处的切线在y轴上的截距.(Ⅰ)求y(x)；(Ⅱ)求函数f(x)=y(t)dt在(0,+∞)上的最大值.

分块矩阵

设A,B为n阶实矩阵，下列结论不成立的是【】

设A,B,C,D都是n×n矩阵，且|A|≠0,AC=CA，证明=|AD-CB|.

已知矩阵A=，若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵，则P,Q可以分别取【】

求微分方程x dy/dx=x-y满足条件 y|x=√2 =0的解.

求微分方程y''+2y'+y=xex的通解（一般解）.

设f(t)=⁡t(1+1/x)2x，则f' (t)=________________.

(1/√x)tanx =__________.

设f(x)与g(x)在(-∞,+∞)上皆可导，且f(x)<g(x)，则必有【】

若y=f(x)，有f'(x0)=1/2，则当∆x→0时，该函数在x=x0处的微分dy是【】

已知y=1+xexy，求 y'|x=0及y''|x=0.

矩阵

设A = aij为3阶矩阵，Aij为代数余子式，若A的每行元素之和均为2，且|A| = 3，A11 + A21 + A31 = ______.

已知A=(1) 求正交矩阵P，使得PTAP为对角矩阵；(2) 求正定矩阵C，使得C2 = (a+3)E-A.

若x=(-1,2,3,0,4)，求‖x‖1,‖x‖2,‖x‖∞.

设A=，求‖x‖1,‖x‖F,‖x‖∞.

设A是n阶矩阵，A*为A的伴随矩阵，证明秩R(A*)与R(A)之间满足R(A* )=

设A=(aij)是n阶实对称正定矩阵，b1,b2,…,bn为任意非零实数，证明B=(aijbibj)也是正定的。

设A为任一n阶矩阵，数λ>0，证明λI+AT A为正定矩阵。

设A≠0，证明：R(A)=1的充要条件是A可表示为一个列向量与一个行向量的乘积。

若n维列向量α与β正交，A=αβT，则A的特征值全为零。

已知A=,B为三阶方阵，满足A2B=A+AB，求B。