大学数学-考研试题(理工数学Ⅱ 1988年求导公式)

填空题（1988年理工数学Ⅱ）

设f(t)=⁡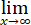t(1+1/x)^2x，则f' (t)=________________.

答案解析

e^2t+2te^2t

讨论

求导公式

y=x1/x，则dy/dx=__________。

设y=ln⁡(1+ax)，其中a是非零常数，则y'=__________，y''=__________.

已知y=1+xexy，求 y'|x=0及y''|x=0.

设f(x)=x(x+1)(x+2)∙⋯∙(x+n)，则f'(0)=____________.

求微分方程x dy/dx=x-y满足条件 y|x=√2 =0的解.

求微分方程y''+2y'+y=xex的通解（一般解）.

已知曲线L的极坐标方程为r=sin3θ(0≤θ≤π/3)，则L围成有界区域的面积为__________.

设A为3阶矩阵，交换A的第2行和第3行，再将第2列的-1倍加第1列，得到矩阵，则A-1的迹tr(A-1)=__________.

设函数y=f(x)是微分方程2xy'-4y=2lnx-1满足条件y(1)=1/4的解，求曲线y=y(x)(1≤x≤e)的弧长.

已知矩阵A=，若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵，则P,Q可以分别取【】

函数的求导法则

设函数g(x)在x=0的领域内有定义，g(0)=g'(0)=0,f(x)=，求f'(0).

设f(t)=t(1+1/x)2tx ，则f' (t)=__________.

设y=etan⁡(1/x) ∙sin(1/x)，则y'=________________.

已知y=arcsine-√x，求y'.

微分方程y''' - y = 0的通解y=_____________________.

多项式f(x)=中x3项的系数为______.

f(x)满足∫f(x)/dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A，求s和A.

设函数y=y(x)的微分方程xy' - 6y = -6，满足y()=10,(1) 求y(x);(2) P为曲线y=y(x)上的一点，曲线y=y(x)在点P的法线在y轴上的截距为Iy，为使Iy最小，求P的坐标.

∫f'(x)dx=__________.

设，求dy/dx,(d2 y)/(dx2 ).

导数与微分

设f(x)=(n=1,2,3,…)，求f(n)(x).

设y=ln(1-x2)，求y(n).

若f(x),g(x)在[a,b]上可导，∀x∈[a,b],f' (x)≤g'(x)，则∀x∈[a,b],f(x)≤g(x).

设f(x)在[a,b]上单调，证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.

由方程xyz+=√2所确定的函数z=z(x,y)在点(1,0,-1)处的全微分dz=____________.

设函数y=y(x)由方程ex+y+cos⁡(xy)=0确定，则dy/dx=__________.

设函数f(x)在(-∞,+∞)内有定义，对任意x都有f(x+1)=2f(x)，且当0≤x≤1时f(x)=x(1-x2)，试判断在x=0处函数f(x)是否可导.

设f(x)可导，F(x)=f(x)(1+|sinx|)，欲使F(x)在x=0可导，则必有【】

设当x=0时，f(sinx)= f2(sinx)，f'(x)≠0，则f(0)=__________.

已知函数y=f(x)在x=2处连续，且=2求证f(x)在x=2处可导，并求f'(x)=2.