已知y=arcsine-√x,求y'.
设函数g(x)在x=0的领域内有定义,g(0)=g'(0)=0,f(x)=,求f'(0).
设y=ln(1+ax),其中a是非零常数,则y'=__________,y''=__________.
设f(t)=t(1+1/x)2x,则f' (t)=________________.
设f(t)=t(1+1/x)2tx ,则f' (t)=__________.
设f(x)=x(x+1)(x+2)∙⋯∙(x+n),则f'(0)=____________.
设y=etan(1/x) ∙sin(1/x),则y'=________________.
求∫dx/(a2sin2x+b2cos2x ).( a,b是不全为零的非负常数)
设3阶矩阵A=(α1,α2,α3),B=(β1,β2,β3),若向量组α1,α2,α3可以由向量组β1,β2线性表出,则【 】
设函数f(x)在(-∞,+∞)内有定义,对任意x都有f(x+1)=2f(x),且当0≤x≤1时f(x)=x(1-x2),试判断在x=0处函数f(x)是否可导.
设f(x)可导,F(x)=f(x)(1+|sinx|),欲使F(x)在x=0可导,则必有【 】
设当x=0时,f(sinx)= f2(sinx),f'(x)≠0,则f(0)=__________.
设f(x)在[a,b]上单调,证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.
由方程xyz+=√2所确定的函数z=z(x,y)在点(1,0,-1)处的全微分dz=____________.
设函数y=y(x)由方程ex+y+cos(xy)=0确定,则dy/dx=__________.
已知函数y=f(x)在x=2处连续,且=2求证f(x)在x=2处可导,并求f'(x)=2.
已知矩阵A=,若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵,则P,Q可以分别取【 】
设f(x)在x=a处可导,则(f(a+x)-f(a-x))/x等于【 】
有一圆柱体底面半径与高随时间变化的速率分别为2cm/s,-3cm/s,当底面半径为10cm,高为5cm时,圆柱体的体积与表面积随时间变化的速率分别为【 】
设函数z=z(x,y)由方程(x+1)z+ylnz-arctan(2xy)=1确定,则 = ______.
微分方程y''' - y = 0的通解y=_____________________.
设矩阵A=仅有两个不同的特征值.若A相似于对角矩阵,求a,b的值,并求可逆矩阵P,使P-1AP为对角矩阵.
求微分方程y'+1/x y=1/(x(x2+1))的通解(一般解).
f(x)满足∫f(x)/dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A,求s和A.


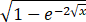 ∙e-√x∙(-1)/(2√x)=-e-√x/(2√x
∙e-√x∙(-1)/(2√x)=-e-√x/(2√x 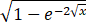 ).
).