多项式f(x)=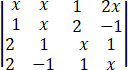
中x3项的系数为______.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设A为n阶非零方阵，A*是A的伴随矩阵，AT的转置矩阵，当A*=AT时，证明|A|≠0.
已知二次型f(x1,x2,x3 )=3x12+4x22+3x32+2x1 x3，(1)求正交变换x=Qy将f(x1,x2,x3)化为标准形；(2)证明minx≠0f(x)/(xT x)=2.
将长为a的铁丝切成两段，一段围成正方形，另一段围成圆，问这两段铁丝长各为多少时，正方形与圆的面积之和为最小？
若3a2-5b<0，则方程x5+2ax3+3bx+4c=0【 】
设两函数f(x)及g(x)都在x=a处取得极大值，则函数F(x)=f(x)g(x)在x=a处【 】
在椭圆x2/a2 +y2/b2 =1的第一象限上求一点P，使该点处的切线、椭圆及两坐标轴所围成图形面积为最小（其中a>0,b>0）.
设f(x)=x3+6x2+3px+8，试确定p的值使f(x)有重根并求其根.
设复系数多项式f(x)在x=1处的导数f'(1)≠0.证明：存在n阶复方阵A使得f(A)=f(1)J，其中J=是n阶Jordan块.
已知线性方程组有解，其中a,b为常数.若=4，则=__________.
证明：如果d(x)|f(x),d(x)|g(x)，且d(x)是f(x)与g(x)的一个组合，那么d(x)是f(x)与g(x)的一个最大公因式.
设A=是实数域上的矩阵，证明：(1)如果|aii|>∑j≠i|aij|,i=1,2,…,n则|A|≠0;(2)如果aii>∑j≠i|aij|,i=1,2,…,n则|A|>0.
设A∈Cn×n,W={f(A):f(x)∈P[x]},m(x)是A的最小多项式，证明：W的维数=∂(m(x))，其中∂(m(x))表示m(x)的最高次数.
设A,B都是n阶复方阵，C=A+B，则det(C-AB)=det(C-BA).
设4阶矩阵A=(α,γ2,γ3,γ4 ),B=(β,γ2,γ3,γ4)，其中α,β,γ2,γ3,γ4均为四维列向量，且已知行列式|A|=4,|B|=1，则行列式|A+B|=________.
三阶行列式有2个元素为4，其余为±1，则此行列式可能的最大值为________.
设γ1,γ2,α,β皆为三维列向量，A=(α,3γ1,3γ2 ),B=(β,γ1,2γ2)且|A|=18,|B|=4，则|A-B|=________.
设A为n阶方阵，且A的行列式|A|=a≠0，而A*是A的伴随矩阵，则|A* |等于【 】