大学数学-考研试题(重庆大学 2005年克拉默法则)

计算题（2005年重庆大学）

计算行列式：.

答案解析

暂无答案

讨论

克拉默法则

A为4阶方阵，且|A|=-2，则||A|A|=【】

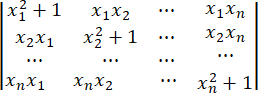定义函数f(x)在[a,b]可积时，必须选假定f(x)在[a,b]上有界.

设f(x)在[a,b]上可积，则f(x)在[a,b]上的连续点有无限多个.

三阶方阵A的特征值为1,-1,2，则A2+4A-1的特征值=________.

设A=是实数域上的矩阵，证明：(1)如果|aii|>∑j≠i|aij|,i=1,2,…,n则|A|≠0;(2)如果aii>∑j≠i|aij|,i=1,2,…,n则|A|>0.

求不定积分∫(ln⁡(1+x2))/x3 dx

连续函数的不定积分一定存在.

三阶行列式有2个元素为4，其余为±1，则此行列式可能的最大值为________.

设γ1,γ2,α,β皆为三维列向量，A=(α,3γ1,3γ2 ),B=(β,γ1,2γ2)且|A|=18,|B|=4，则|A-B|=________.

若A=相似于对角阵，则a与b的关系为________.

行列式

五阶行列式D5==__________。

设A=(aij)n×n，且行列式≠0,1≤k≤n.证明存在下三角形矩阵Bn×n，使BA为上三角形矩阵。

计算行列式的值：Dn=

若不可约多项式p(x)是f(k)(x)的s重因子，且p(x)|f(x)，那么p(x)________ f(x)的s+k重因子.

证明：如果d(x)|f(x),d(x)|g(x)，且d(x)是f(x)与g(x)的一个组合，那么d(x)是f(x)与g(x)的一个最大公因式.

设A∈Cn×n,W={f(A):f(x)∈P[x]},m(x)是A的最小多项式，证明：W的维数=∂(m(x))，其中∂(m(x))表示m(x)的最高次数.

设a1,a2,…,an是n个实数，证明：|ai|≤.

多项式f(x)=中x3项的系数为______.

已知线性方程组有解，其中a,b为常数.若=4，则=__________.

设A为n阶非零方阵，A*是A的伴随矩阵，AT的转置矩阵，当A*=AT时，证明|A|≠0.

行列式的计算

设A是m×n矩阵，B是n×m矩阵，则【】

设A是n阶矩阵，满足AAT=E(E是n阶单位矩阵，AT是A的转置矩阵)，|A|<0，求|A+E|.

设A,B都是n阶复方阵，C=A+B，则det(C-AB)=det(C-BA).

4阶行列式的值等于【】

设4阶矩阵A=(α,γ2,γ3,γ4 ),B=(β,γ2,γ3,γ4)，其中α,β,γ2,γ3,γ4均为四维列向量，且已知行列式|A|=4,|B|=1，则行列式|A+B|=________.

设A为n阶方阵，且A的行列式|A|=a≠0，而A*是A的伴随矩阵，则|A* |等于【】

设A为m×n矩阵，非齐次线性方程组Ax ̅=β ̅有唯一解的充分必要条件为：______________.

设f(x)=，则f(x)=0的根为____________.

向量组α1=(1 1 k),α2=(1 k 1),α3=(k 1 1)是线性无关的，则k=__________.

已知四维实矢量空间的矢量（表示成矩阵）：=,满足如下条件：以及T∙=9/4（其中，T表示对矩阵取置换），试求出所有这样的四维实矢量的集合：{ }=?