设矩阵A=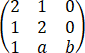
仅有两个不同的特征值.若A相似于对角矩阵，求a,b的值，并求可逆矩阵P，使P-1AP为对角矩阵.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2021年理工数学Ⅱ；2021年经济数学Ⅲ）
答案解析
|λE-A|==(λ-b)(λ-3)(λ-1)=0 当b=3时，由A相似对角化可知，二重根所对应特征值至少存在两个线性无关的特征向量，(3E-A)=,a=-1，此时, λ1=λ2=3所对应特征向量为α...
查看完整答案讨论
设A=E-ξξT，其中E是n阶单位矩阵，ξ是n维非零列向量，ξT是ξ的转置，证明：(1)A2=A的充要条件是ξTξ=1;(2)当ξTξ=1时，A是不可逆矩阵.
设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B.(1)证明B可逆；(2)求AB-1.
设A为方阵，g(λ)是A的最小多项式，f(λ)为任意多项式.证明：f(A)可逆⇔(f(λ),g(λ))=1.
设4阶方阵A=，则A的逆矩阵A-1=____________.
设矩阵T=,T以及D可逆，证明(A-BD-1 C)-1存在，并求T-1，其中A,B,C,D为适当维度的矩阵。
设矩阵A=,E=，则逆矩阵(A-2E)-1=________.
已知二次型f(x1,x2,x3 )=3x12+4x22+3x32+2x1 x3，(1)求正交变换x=Qy将f(x1,x2,x3)化为标准形；(2)证明minx≠0f(x)/(xT x)=2.
设函数f(x)=ax-blnx(a>0)有两个零点，则b/a的取值范围是【 】
设A是2022阶可逆对称实方阵，则A必有2021阶非零主子式
设A = aij为3阶矩阵，Aij为代数余子式，若A的每行元素之和均为2，且|A| = 3，A11 + A21 + A31 = ______.
设A,B为n阶可逆矩阵，E为n阶单位矩阵，M*为M的伴随矩阵，则=【 】
设A=,A*为A的伴随矩阵，则|(1/4 A)-1 - 15A* |=________.
设n阶方阵A,B,C满足关系式ABC=E，其中E是n阶单位矩阵，则必有【 】
设A=，其中a_i≠0,b≠0(i=1,2,⋯,n)，则矩阵A的秩r(A)=________.
已知α=[1,2,3],β=[1,1/2,1/3]，设A=αTβ，其中αT是α的转置，则An=________________.