已知f(x)=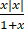
，求f(x)的凹凸性及渐近线.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2021年理工数学Ⅱ）
答案解析
因为f(x)=，故x>0时，f' (x)=(2x+x2)/(1+x)2 ,f'' (x)=2/(1+x)3 ，x<0时，f' (x)=(-2x-x2)/(1+x)2 ,f'' (x)=(-2)/(1+x)3 ,所以凹区间(-∞,1)，(0,+...
查看完整答案讨论
微分方程y''' - y = 0的通解y=_____________________.
已知函数f(t)=dxsin(x/y)dy，则f'(π/2)=______.
设函数z=z(x,y)由方程(x+1)z+ylnz-arctan(2xy)=1确定，则 = ______.
已知矩阵A=，若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵，则P,Q可以分别取【 】
设3阶矩阵A=(α1,α2,α3)，B=(β1,β2,β3)，若向量组α1,α2,α3可以由向量组β1,β2线性表出，则【 】
设函数f(x)=secx在x=0处的2次泰勒多项式为1+ax+bx2，则【 】
设函数f(x)=ax-blnx(a>0)有两个零点，则b/a的取值范围是【 】
有一圆柱体底面半径与高随时间变化的速率分别为2cm/s，-3cm/s，当底面半径为10cm，高为5cm时，圆柱体的体积与表面积随时间变化的速率分别为【 】
设函数f(x)在(0,+∞)上连续可导，f(x)存在，f(x)的图形在(0,+∞)是上凸的，求证：f′(x)=0.
确定函数y=(x+1)/x2 的单调区间、极值、凸凹区间、拐点以及渐近线.
设在区间[a,b]上f(x)>0,f' (x)<0,f''(x)>0，记S1=f(x)dx,S2=f(b)(b-a),S3=1/2[f(a)+f(b)](b-a)，则【 】
曲线y=(t-1)(t-2)dt在点(0,0)处的切线方程是____________.
设f(x)有二阶连续导数，且f' (0)=0,f''(x)/|x|=1，则【 】
曲线y=arctanx在横坐标为1的点处的切线方程是__________；法线方程是____________.
求函数f(x)=x2/(1+x2 )的极值与拐点，并求拐点处的切线方程.
设函数f(x)在开区间(a,b)内存在二阶导数f''(x)，且在(a,b)内f''(x)>0，证明：对于任意两点x1,x2∈(a,b)，恒有f((x1+x2)/2)≤(f(x1)+f(x2))/2.
设x>0时，f(x)=，求证：x→0+时，f(x)=e+Ax+Bx2+o(x2)，并求A,B之值.
设函数f(x)=sinx/(1+x2)在x=0处的3次泰勒多项式为ax+bx2+cx3，则【 】
设函数f(x)在区间[0,1]上连续，则f(x)dx=【 】
设f(x)在[0,1]上具有二阶导数，且满足条件|f(x)|≤a,|f''(x)|≤b，其中a,b都是非负常数，c是(0,1)内任意一点，证明：|f'(c)|≤2a+b/2.
已知f(x)在[a,b]上二阶可导，且f''(x)≤0，证明：f(x)dx≤(b-a)f((a+b)/2).
设f:[0,1]→[0,1]是一个连续函数，证明：方程2x-f(t)dt=1在[0,1]中有且仅有一个零点.
求证不等式：(eb - ea)/(b-a)<(eb + ea)/2 (a≠b).