设函数f(x)在区间[0,1]上连续,则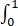 f(x)dx=【 】
f(x)dx=【 】
A、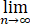
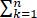 f(
f(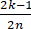 )
)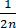
B、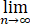
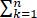 f(
f(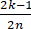 )
)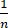
C、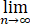
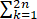 f(
f(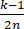 )
)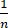
D、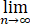
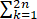 f(
f(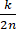 )
)
设函数f(x)=sinx/(1+x2)在x=0处的3次泰勒多项式为ax+bx2+cx3,则【 】
设函数f(x,y)可微,且f(x+1,ex)=x(x+1)2 , f(x,x2)=2x2lnx,则df(1,1)=【 】
已知 fn(x)=求证:(1)对于任何自然数n,方程fn(x)=在区间(0,)中仅有一根;(2)设xn∈(0,)满足fn(xn)=,则.
证明:[x3]+x2=[x2]+x3存在一个非整数解,其中[x]表示不大于x的最大整数.
设函数f(x)在(0,1)上有定义,且函数exf(x)与函数e-f(x)在(0,1)上都是单调递增的,求证:f(x)在(0,1)上连续.
设x>0时,f(x)=,求证:x→0+时,f(x)=e+Ax+Bx2+o(x2),并求A,B之值.
已知f(x)在[a,b]上二阶可导,且f''(x)≤0,证明:f(x)dx≤(b-a)f((a+b)/2).
当x→0时,x-sinxcosxcos2x与cx4为等价无穷小,则c=__________,k=__________.
当x→0时,1-cosxcos2xcos3x对于无穷小x的阶数等于 __________.
设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f''(x)|≤b,其中a,b都是非负常数,c是(0,1)内任意一点,证明:|f'(c)|≤2a+b/2.
设函数f(x)=secx在x=0处的2次泰勒多项式为1+ax+bx2,则【 】
设x1=10,xn+1=(n=1,2,⋯),试证数列{xn}的极限存在,并求此极限.
设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f''(x)|≤b,其中a,b都是非负常数,c是(0,1)内任意一点,证明:|f'(c)|≤2a+b/2.
设f:[0,1]→[0,1]是一个连续函数,证明:方程2x-f(t)dt=1在[0,1]中有且仅有一个零点.
求证不等式:(eb - ea)/(b-a)<(eb + ea)/2 (a≠b).
证明:若f(x)在区间(a,b)内可导且无界,则其导函数f'(x)在(a,b)内也无界,但反之不然,举出例子.
试求椭圆x2/4+y2=1上一点,使其到直线3x+4y-12=0,3x-4y+12=0和y+3=0的距离平方和最小.
已知函数f(x)在(0,1)上连续,且f(1)=3ex-1f(x)dx,证明:存在ξ∈(0,1),使得f(ξ)+f'(ξ)=0.
已知f(x)在[a,b]上三次可微,且f(a)=f' (a)=f(b)=0,|f''' (x)|≤M,证明:|f(x) dx|≤M/72 (b-a)4.
设a,b,c,d皆为常数,cd≠0,说明并给出理由,当a,b,c,d满足什么条件时,f(x)=(ax+b)/(cx+d)无极值.