设x1=10,xn+1=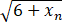
(n=1,2,⋯)，试证数列{xn}的极限存在，并求此极限.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（1996年理工数学Ⅰ）
答案解析
由x1=10,x2==4知，x1>x2.设对某个正整数k有xk>xk+1，则xk+1=>=xk+2,故由数学归纳法知，对一切正整数n，都有xn>xn+1，即数列{xn}为单调减少数列.又显然有xn>0(...
查看完整答案关注优题吧，注册平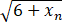台账号.
设x1=10,xn+1=(n=1,2,⋯)，试证数列{xn}的极限存在，并求此极限.
由x1=10,x2==4知，x1>x2.设对某个正整数k有xk>xk+1，则xk+1=>=xk+2,故由数学归纳法知，对一切正整数n，都有xn>xn+1，即数列{xn}为单调减少数列.又显然有xn>0(...
查看完整答案