当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
A、x•o(x2)=o(x3)
B、o(x)•o(x2)=o(x3)
C、o(x2)+o(x2)=o(x2)
D、o(x)+o(x2)=o(x2)
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
单项选择（2013年考研）
答案解析
D
【解析】
假设o(x)+o(x²)=o(x²)，根据高阶无穷小定义，有
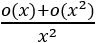=0.
事实上，
=
=
讨论
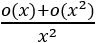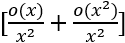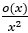
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
设f(x)=在(-∞,+∞)内连续，则a=________.
设f(x)=在x=0处连续，则常数a与b应满足的关系是__________.
设F(x)=，其中f(x)在x=0处可导，f' (0)≠0,f(0)=0，则x=0是F(x)的【 】
设 f(x) 是连续函数，F(x)是 f(x)的原函数，则【 】
试问函数f(x,y)=sin[π/(1-x2-y2 )]在区域D:{(x,y)∈R2;x2+y2<1}上是否一致连续？证明你的结论.
在平面直角坐标系中，椭圆x2+xy+y2=1的长轴方程为__________，位于x轴上半平面内的焦点坐标为__________.
若函数f(x)在[0,1]上连续，f(0)=0,f(1)=1，则对任何自然数n≥1，存在ξ_n∈[0,1]，使得f(ξn+1/n)=f(ξn )+1/n.
已知函数f(x)在[a,+∞)上连续，且f(x)存在，证明：(1)函数f(x)有界；(2)存在ξ∈[a,+∞)，使得f(ξ)为f(x)在[a,+∞)上的最大值或最小值.