设f(x)有连续的导数,f(0)=0,f'(0)≠0,F(x)=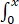 (x2-t2) f(t)dt,且当x→0时,F'(x)与xk是同阶无穷小,则k等于【 】
(x2-t2) f(t)dt,且当x→0时,F'(x)与xk是同阶无穷小,则k等于【 】
A、1
B、2
C、3
D、4
设f(x)有连续的导数,f(0)=0,f'(0)≠0,F(x)=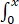 (x2-t2) f(t)dt,且当x→0时,F'(x)与xk是同阶无穷小,则k等于【 】
(x2-t2) f(t)dt,且当x→0时,F'(x)与xk是同阶无穷小,则k等于【 】
A、1
B、2
C、3
D、4
C
设an>0(n=1,2,⋯),且an 收敛,常数λ∈(0,π/2),则级数(-1)n (ntan λ/n) a2n【 】
设f(x)有二阶连续导数,且f' (0)=0,f''(x)/|x|=1,则【 】
已知((x+ay)dx+ydy)/(x+y)2 为某函数的全微分,则a等于【 】
设ξ,η是两个相互独立且均服从正态分布N(0,1/2)的随机变量,则随机变量|ξ-η|的数学期望E(|ξ-η|)=________.
设工厂A 和工厂B的产品的次品率分别为1% 和 2%,现从由 A 厂和 B厂的产品分别占60% 和 40% 的一批产品中随机抽取一件,发现是次品,则该次品属 A厂生产的概率是________.
设A是4×3矩阵,且A的秩r(A)=2,而B=,则r(AB)=________.
函数u=ln(x+)在A(1,0,1)处沿A点指向B(3,-2,2)点方向的方向导数为________.
微分方程y''-2y'+2y=ex的通解为____________.
能否用迭代法求下列方程,如不能,将方程改写为能用迭代法求解的形式.x=4-αx.
若z=x+iy,f(z)=u(x,y)+iv(x,y)解析,且u-v=(x-y)(x2+4xy+y2),求f(z).
对∀p为正整数,|un+p - un |=0,则un 存在.
设xn=1+1/√3+1/√5+⋯+1/ - ,证明xn 存在.
设f(x)=,f[φ(x)]=1-x,且φ(x)≥0,求φ(x)及其定义域.
f(x)=|xsinx| ecosx,-∞<x<+∞是【 】
设函数f(x)=,则函数f[f(x)]=__________.