设f(x)=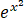
,f[φ(x)]=1-x，且φ(x)≥0，求φ(x)及其定义域.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（1988年理工数学Ⅰ；1988年理工数学Ⅱ）
答案解析
由f(x)=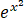,f[φ(x)]=1-x，有
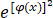=1-x，解得φ(x)=
.
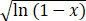其定义域为ln(1-x)≥0得1-x≥1，即x≤0.
讨论
n维向量组α1,α2,…,αs (3≤s≤n)线性无关的充要条件是【 】
设幂级数an(x-1)n在x=-1处收敛，则此级数在x=2处【 】
设空间区域Ω1:x2+y2+z2≤R2,z≥0,Ω2:x2+y2+z2≤R2,x≥0,y≥0,z≥0，则【 】
设y=f(x)是方程y''-2y'+4y=0的一个解，且f(x0)>0,f' (x0)=0，则函数f(x)在点x0处【 】
若函数y=f(x)可导，且f'(x0)=1/2，则当∆x→0时，该函数在x=x0处的微分dy是【 】
设4阶矩阵A=(α,γ2,γ3,γ4 ),B=(β,γ2,γ3,γ4)，其中α,β,γ2,γ3,γ4均为四维列向量，且已知行列式|A|=4,|B|=1，则行列式|A+B|=________.
设f(x)连续，且f(t)dt=x，则f(7)=______.
设f(x)是周期为2的周期函数，它在区间(-1,1]上定义为f(x)=，则f(x)的傅里叶级数在x=1处收敛于______.
已知φ(x)=|x-t|f(t)dt，若积分存在，且f(x)>0，证明：φ(x)为[a,b]上的凸函数.
若z=x+iy,f(z)=u(x,y)+iv(x,y)解析，且u-v=(x-y)(x2+4xy+y2)，求f(z).
已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=____________________.
函数y=sinx|sinx|（其中|x|≤π/2）的反函数为____________________.
设a1=1,an=sinan-1 (n≥2)，证明：an≥(n≥2).
能否用迭代法求下列方程，如不能，将方程改写为能用迭代法求解的形式.x=4-αx.
设函数f(x)在[a,b]上有定义，在(a,b)上连续.下面哪个条件能够判定函数f(x)在[a,b]上有最大值【 】
在平面直角坐标系中，椭圆x2+xy+y2=1的长轴方程为__________，位于x轴上半平面内的焦点坐标为__________.