设fn (x)在(a,b)上单调递增,且有实数列{Mn },n=1,2,3,…使得∀x∈(a,b),|fn (x)|≤Mn,若fn (x)在(a,b)上一致收敛于f(x),证明:
(1)存在M>0,使得∀x∈(a,b),|f(x)|≤M;
(2)极限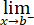 f(x)存在.
f(x)存在.
设fn (x)在(a,b)上单调递增,且有实数列{Mn },n=1,2,3,…使得∀x∈(a,b),|fn (x)|≤Mn,若fn (x)在(a,b)上一致收敛于f(x),证明:
(1)存在M>0,使得∀x∈(a,b),|f(x)|≤M;
(2)极限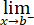 f(x)存在.
f(x)存在.
暂无答案
设xoy在平面上n个结点Mi(xi,yi ),i=1,2,…,n(n≥3).证明:M1,M2,…,Mn在同一条直线上⟺R=2.
设σ为n维线性空间V的一个线性变换,σ2=σ,证明:(1)σ特征值为0,1;(2)设V0,V1分别为0,1对应的特征子空间,则V=V0⊕V1;(3)若σ只有0特征值,则σ为零变换.
设A为n阶方阵,A*为A的伴随矩阵且A11≠0,b≠0,其中A11为A的a11对应的代数余子式.证明:AX=b有无穷多个解⟺b是A* X=0的解.
已知同维数的两个向量组有相同的秩,且其中之一可用另外一个线性表示,证明:这两个向量组等价。
设A是n阶正定矩阵,B为n阶实方阵,证明:(1)若B'=B,则AB的特征值为实数;(2)若B正定,则AB的特征值皆大于0;(3)若B正定,且AB=BA,则AB正定。