已知α>0,求极限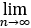
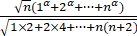
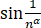 .
.
已知f(x)=,将f(x)展开成正弦级数,并求该级数的和函数.
已知u是Ω=[0,1]×[0,1]×[0,1]上的正值连续函数,Ip(u)=(∭Ωupdxdydz)1/p证明:Ip(u)=
已知{un(x)}是可微函数列,且un(x)在[a,b]上一致有界,证明:若un(x)收敛,则un(x)必定一致收敛.
已知含参变量积分F(x)=sin(xy)/(ln(lny)) dy,证明:(1) F(x)在[δ,+∞)上关于x一致收敛(δ>0)(2) F(x)在(0,+∞)上关于x不一致收敛.
已知f(x)在[a,b]上三次可微,且f(a)=f' (a)=f(b)=0,|f''' (x)|≤M,证明:|f(x) dx|≤M/72 (b-a)4.
已知S={(x,y,z)│x2+4y2+9z2=1,z≤0}取下侧,求∬S(yez+x)dydz+(zex+y)dzdx+(xcosxy+z)dxdy


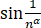 ~1/nα (n→∞)
~1/nα (n→∞) =
=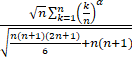
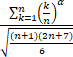 =
=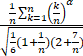
 =√3
=√3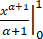 =√3/(α+1)
=√3/(α+1)