求极限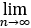 (
(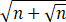 -√n)/
-√n)/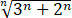
计算题(2022年北京理工大学)
答案解析
分子、分母同乘以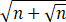 +√n:
+√n:
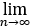 (
(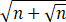 -√n)(
-√n)(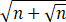 +√n)/
+√n)/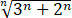 (
(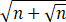 +√n))
+√n))
=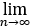 √n/
√n/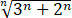 (
(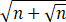 +√n))
+√n))
=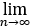 1/
1/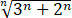 (√(1+1/√n)+1) )
(√(1+1/√n)+1) )
=1/2 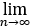 1/
1/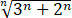 =1/2×1/3
=1/2×1/3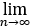 1/
1/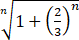 =1/6
=1/6
讨论
求证:J=ln(sinx)dx收敛且J=-π/2 ln2.
设f∈[0,2π],证明:f(x)|sinnx|dx=2/πf(x)dx.
若函数f(x)在[0,1]上连续,f(0)=0,f(1)=1,则对任何自然数n≥1,存在ξ_n∈[0,1],使得f(ξn+1/n)=f(ξn )+1/n.
求∫C1/(xdx+ydy),其中C是从(1,0)到(0,2)的光滑曲线(不过原点).
求∫Cx2ds,其中C为x2+y2+z2=a2 (a>0)与z=的交线.
试求椭圆x2/4+y2=1上一点,使其到直线3x+4y-12=0,3x-4y+12=0和y+3=0的距离平方和最小.
设f(x)有连续的导数,f(0)=0,f'(0)≠0,F(x)=(x2-t2) f(t)dt,且当x→0时,F'(x)与xk是同阶无穷小,则k等于【 】
设 f(x) 是连续函数,F(x)是 f(x)的原函数,则【 】
设函数f(x)在[a,b]上有定义,在(a,b)上连续.下面哪个条件能够判定函数f(x)在[a,b]上有最大值【 】
设函数f:R→R满足:(1) f(1)=1,(2) f'(x)=1/(x2+[f(x)]2),∀x≥1.证明:f(x)存在且小于1+π/4.
在平面直角坐标系中,椭圆x2+xy+y2=1的长轴方程为__________,位于x轴上半平面内的焦点坐标为__________.
设函数f(x)=x-[x],其中[x]表示不超过x的最大整数,求极限1/xf(x)dx.

