设数列{xn}满足0<x1<π，xn+1=sinxn（n=1,2,...）.证明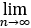
xn存在，并求该极限.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（2006年考研）
答案解析
由0<x1<π，可知x2=sinx1∈（0，1）⊂（0，π/2），于是对于∀n≥2，有xn∈（0，1），故数列{xn}有界.又当x≥0时，得sinx≤x，所以xn+1=sinxn≤xn，即...
查看完整答案讨论
设f(x)=sin(a1 x)+sin(a2 x)+sin(a3 x),a1,a2,a3>0.证明：存在数列{tn}使得tn=+∞且f(x+tn)=f(x)对∀x∈R一致成立.
设xn=1+1/√3+1/√5+⋯+1/ - ，证明xn 存在.
设x1=10,xn+1=(n=1,2,⋯)，试证数列{xn}的极限存在，并求此极限.
已知an=-(-1)n/n(n=1,2,…)，则{an}【 】
对有界数列{xn}，下面哪个说法可作为xn=L的定义【 】（此题不全，待更新）
已知an=+∞，证明(a1+a2+⋯+an)/n=+∞，并举例说明反过来不成立.
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
设函数f(x)在[0,+∞)连续，(f(x)-k√x)=0,k>0为常数，证明：f(x)在[0,+∞)上一致连续.
设函数f(x)=，试定义f(1)的数值，使f(x)在x=1连续.
设f(x)=在(-∞,+∞)内连续，则a=________.
设f(x)=在x=0处连续，则常数a与b应满足的关系是__________.
设F(x)=，其中f(x)在x=0处可导，f' (0)≠0,f(0)=0，则x=0是F(x)的【 】
试问函数f(x,y)=sin[π/(1-x2-y2 )]在区域D:{(x,y)∈R2;x2+y2<1}上是否一致连续？证明你的结论.
若函数f(x)在[0,1]上连续，f(0)=0,f(1)=1，则对任何自然数n≥1，存在ξ_n∈[0,1]，使得f(ξn+1/n)=f(ξn )+1/n.