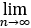 (1+22√2+32∛3+⋯+n2
(1+22√2+32∛3+⋯+n2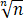 )/n3
)/n3
计算题(2022年中国科学院)
答案解析
设yn=1+22 √2+32 ∛3+⋯+n2 ,xn=n3,则{xn },{yn}严格递增,且xn→∞,yn→∞(n→∞).∵(yn-yn-1)/(xn-xn-1 )=(n2 )/(n3-(n-1)3...
查看完整答案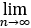 (1+22√2+32∛3+⋯+n2
(1+22√2+32∛3+⋯+n2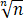 )/n3
)/n3
设yn=1+22 √2+32 ∛3+⋯+n2 ,xn=n3,则{xn },{yn}严格递增,且xn→∞,yn→∞(n→∞).∵(yn-yn-1)/(xn-xn-1 )=(n2 )/(n3-(n-1)3...
查看完整答案