求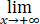 √x
√x 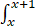 dt/
dt/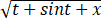 .
.
计算题(1995年南京大学)
答案解析
应用定积分的保向性,有
φ(x)=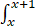 dt/
dt/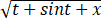 ≤
≤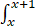 dt/
dt/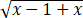 =1/
=1/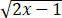
φ(x)=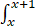 dt/
dt/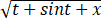 ≥
≥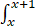 dt/
dt/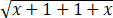 =1/
=1/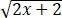
因为
 √x 1/
√x 1/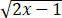 =1/√2,
=1/√2, √x 1/
√x 1/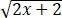 =1/√2
=1/√2
应用夹逼准则得
原式= √x φ(x)=1/√2.
√x φ(x)=1/√2.
讨论
设函数f(x)在[0,1]上连续,在(0,1)内可导,且3f(x)dx=f(0),证明:在(0,1)内存在一点c,使f'(c)=0.
设M=sinx/(1+x2)cos4x dx,N=(sin3x+cos4x )dx,P=(x2sin3x-cos4x)dx,则有【 】
设I1=x/2(1+cosx) dx,I2=ln(1+x)/(1+cosx) dx,I3=2x/(1+sinx) dx,则【 】
设连续函数f(x)满足f(a+b-x)=f(x),∀x∈[a,b],则积分xf(x)dx等于【 】
证明:xasinxdx∙a-cosx dx≥π³/4其中,a>0为常数.
设f(a)=0,f(x)在[a,b]上的导数连续,求证:1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] |f'(x)|,x∈[a,b]

