d/dx 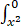 xcost2dt=______________.
xcost2dt=______________.
设A为n阶非零方阵,A*是A的伴随矩阵,AT的转置矩阵,当A*=AT时,证明|A|≠0.
已知点A与B的直角坐标分别为(1,0,0)与(0,1,1).线段AB绕z轴旋转一周所成的旋转曲面为S.求由S及两平面z=0,z=1所围成的立体体积.
设f(x)在x=0的某一领域内具有二阶连续导数,且f(x)/x=0,证明级数f(1/n)绝对收敛.
设f(x)具有二阶连续导数,f(0)=0,f'(0)=1,且[xy(x+y)-f(x)y]dx+[f'(x)+x2y]dy=0为一阶全微分方程,求f(x)及此全微分方程的通解.
计算曲面积分∬S(xdydz+z2dxdy)/(x2+y2+z2 ),其中S是由曲面x2+y2=R2及平面z=R,z=-R(R>0)所围成的立体表面的外侧.
设f(x)是连续函数,且F(x)=f(t)dt,则F'(x)等于【 】
设函数f(x)在[0,1]上连续,在(0,1)内可导,且3f(x)dx=f(0),证明:在(0,1)内存在一点c,使f'(c)=0.
设f(x)连续,且f(t)dt=x,则f(7)=__________.
设f(x)在(-∞,+∞)内连续可导,且m≤f(x)≤M,a>0.(1)求1/(4a2)[f(t+a)-f(t-a)]dt;(2)求证:|1/2af(t)dt-f(x)|≤M-m.
设M=sinx/(1+x2)cos4x dx,N=(sin3x+cos4x )dx,P=(x2sin3x-cos4x)dx,则有【 】
证明:xasinxdx∙a-cosx dx≥π³/4其中,a>0为常数.
设f(a)=0,f(x)在[a,b]上的导数连续,求证:1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] |f'(x)|,x∈[a,b]


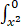 cost2dt - 2x2cosx4
cost2dt - 2x2cosx4