设f(x)是连续函数,且F(x)=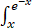 f(t)dt,则F'(x)等于【 】
f(t)dt,则F'(x)等于【 】
A、-e-x f(e-x )-f(x)
B、-e-x f(e-x )+f(x)
C、e-x f(e-x )-f(x)
D、e-x f(e-x )+f(x)
设f(x)是连续函数,且F(x)=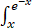 f(t)dt,则F'(x)等于【 】
f(t)dt,则F'(x)等于【 】
A、-e-x f(e-x )-f(x)
B、-e-x f(e-x )+f(x)
C、e-x f(e-x )-f(x)
D、e-x f(e-x )+f(x)
A
已知离散型随机变量X服从参数为2的泊松分布,即P{X=k}=2ke-2/k!,k=0,1,2,…,则随机变量Z=3X-2的期望E(Z)=________.
设随机事件A,B及其和事件A∪B的概率分别是0.4,0.3,0.6,若B ̅表示B的对立事件,那么积事件AB ̅的概率P(AB ̅ )=________.
已知随机变量X的概率密度函数f(x)=1/2 e-|x|,-∞<x<+∞,则X的概率分布函数F(x)=____________.
已知向量组α1=(1,2,3,4),α2=(2,3,4,5),α3=(3,4,5,6),α4=(4,5,6,7),则该向量组的秩是______.
设函数f(x)=,则函数f[f(x)]=__________.
设a为非零常数,则((x+a)/(x-a))x =________.
过点M(1,2,-1)且与直线垂直的平面方程是__________.
设随机变量X与Y独立,且X服从均值为1、标准差(均方差)为√2的正态分布,而Y服从标准正态分布,试求随机变量Z=2X-Y+3的概率密度函数.
设半径为R的球面Σ的球心在定球面x2+y2+z2=a2 (a>0)上,问当R为何值时,球面Σ在定球面内部的那部分的面积最大?