大学数学-考研试题(重庆大学 2005年反常积分的审敛法)

证明题（2005年重庆大学）

证明含参广义积分F(a)=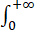e^-axsinxdx在(0,+∞)连续，但非一致收敛.

答案解析

暂无答案

讨论

大学数学

设函数f(x)在[0,+∞)连续、非负，且广义积分f(x)dx收敛，证明：xf(x)dx=0.

设函数f(x)在开区间[0,1]上可微，f(0)=0，且在[0,1]内0<f'(x)<1，证明：(1)对于任意x∈(0,1),f(t)dt>1/2 f2 (x);(2) (f(x)dx)2>f3(x)dx.

设函数f(x)在开区间(a,b)内存在二阶导数f''(x)，且在(a,b)内f''(x)>0，证明：对于任意两点x1,x2∈(a,b)，恒有f((x1+x2)/2)≤(f(x1)+f(x2))/2.

设函数f(x)在闭区间[a,b]上连续，(1)证明：f(x)在[a,b]上一定有最大值和最小值（选最小值证明）；(2)进一步，还假设f(x)在[a,b]上处处不为零，试用定义证明函数1/f2(x)在[a,b]上连续.

(1)设函数f(x)在点x_0点附近有定义，证明：f(x)存在（有限）的充分必要条件是：对任意以x0为极限的数列{xn},xn≠x0，都有数列{f(xn)}收敛；(2)判断极限sin 1/x是否存在（说明理由）.

求由曲面(x2/a2 +y2/b2 +z2/c2 )2=x2/a2 +y2/b2 (a,b,c>0)所围成的空间区域的体积.

设φ(t),ψ(t)有二阶连续导数，u=φ(y/x)+xψ(y/x)，求：x2 ∂2u/∂x2+2xy ∂2u)/∂x∂y+y2 ∂2u/∂y2.

判断函数列fn(x)=(x/n)ln(x/n)在区间(0,1)上的一致收敛性（说明理由）.

求函数f(x)=x2/(1+x2 )的极值与拐点，并求拐点处的切线方程.

求不定积分∫dx/(x3+x2+x+1).

反常积分的审敛法

证明：广义积分lnx/√x dx收敛.

已知f(x)dx条件收敛，且f+(x)=(|f(x)|+f(x))/2,f-(x)=(|f(x)|-f(x))/2证明：(1) f+(x)dx,f-(x)dx均发散到+∞;(2)当A→+∞时，f+(x) dx与f-(x)dx等价.

求积分I(a)=arctan⁡(ax)/(x(1+x2)) dx,a>0.

判断dx/(ex+1)的敛散性.

设[a,+∞)上非负连续函数f可导，且具有连续导函数，若存在r>1，使xf'(x)/f(x)≤-r，证明：反常积分f(x)dx收敛.

讨论sinbx/xλ dx(b≠0)的绝对收敛性和条件收敛性.

先说明广义积分dx/(a4+x4 )收敛（a>0是常数），再计算其积分值.

设p为常数，若反常积分lnx/(xp(1-x)1-p) dx收敛，则p的取值范围是【】

求证：J=ln⁡(sinx)dx收敛且J=-π/2 ln2.

求不定积分∫(ln⁡(1+x2))/x3 dx

定积分

|x|dx = ______.

数值求积f(x)dx时(1)试写出直接用梯形公式的计算式T1；(2)将[a,b]n等分，用Tn表示用复化梯形公式求得的积分值，试写出Tn的计算式；(3)若将步长分半（即步长二分），试给出T2n与Tn的递推关系；(4)若用精度控制|T2n - Tn |<ε，试写出“变步长梯形法”的算法框图.

f(x)在[0,1]上有连续导数，f(x)无零点，且f(0)=1,f(1)=2，则dx= __________。

用Romberge方法求dx的近似值。（给定n=4）

利用δ函数计算下列积分(x2+1)δ(x2-2x-8)dx.

设f(x)在[0,1]上连续，f(x)dx=0,xf(x)dx=1，则存在x0∈[0,1]使|f(x0 )|>4.

(2x+3)/(x2-x+1)dx=__________.

证明：sin⁡(x²)dx>0.

设f(x),g(x)在区间[a,b]上连续，且g(x)取正值，由积分中值定理有f(t)g(t)dt=f(ξ)g(t) dt(a≤ξ≤x≤b)若f+' (a)存在且f+' (a)≠0，求(ξ-a)/(x-a).