大学数学-考研试题(天津大学 2022年反常积分的审敛法)

计算题（2022年天津大学）

求积分I(a)=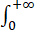arctan⁡(ax)/(x(1+x²)) dx,a>0.

答案解析

∵arctan⁡(ax)/(x(1+x2))=a，∴0不是瑕点.令arctan⁡(ax)/(x(1+x2))|x=0=a，则被积函数在[0,+∞)上连续.被积函数对a求偏导得，∂(arctan⁡(ax)/x(1+x2) )/∂a=1/(1+a2x2)(1+x2) ,在a>0,x≥0的区域连续.下面证明I(a)收敛.∵arctan⁡(ax)/(x(1+x2))≤π/(2x(1+x2)),且π/(2x(1+x2)) dx收敛，∴(arctan⁡(ax))/(x(1+x2)) dx收敛，...

查看完整答案

讨论

大学数学

设级数sinnx/(1+nx2)(1)当x取何值时，级数绝对收敛？并说明理由；(2)当x取何值时，级数条件收敛？并说明理由.

设f(x)=(1)求f(x)的傅里叶级数与傅里叶级数的和函数；(2)证明：1/n2 =π2/6.

设f(x)在(0,1)上可导，在[0,1]上连续，且f(1)-f(0)=2e-1-1.证明：存在ξ∈(0,1)，使得eξ^2 f' (ξ)+2ξ3=0.

设a,b,c,d皆为常数，cd≠0，说明并给出理由，当a,b,c,d满足什么条件时，f(x)=(ax+b)/(cx+d)无极值.

已知f(x)在(-1,1)上有任意阶导数，f(0)=0，且对任意的正整数n都有f(n)(0)=0.设存在C≥0，使得对任意的正整数n和x∈(-1,1)，有|f(n)(x)|≤n!Cn.证明：f(x)在(-1,1)上恒为零.

设f(x)在x=0处连续，且对任意的x∈R，有f(x)=f(3x)，证明：f(x)是常值函数.

证明数列{sinn}发散.

已知函数f(x)在[a,b]上可积，且f(x)=A.对任意的h∈(0,1)，设非负函数g(x,h)满足：⁡g(x,h) dx=1，若对任意的c∈(a,b),g(x,h)在当h→0+关于 x∈[c,b]一致收敛于0，即对∀ε>0,∃δ>0，当0<h<δ时，对∀x∈[c,b]有|g(x,h)|<ε，证明：f(x)g(x,h)dx=A

已知f(x)dx条件收敛，且f+(x)=(|f(x)|+f(x))/2,f-(x)=(|f(x)|-f(x))/2证明：(1) f+(x)dx,f-(x)dx均发散到+∞;(2)当A→+∞时，f+(x) dx与f-(x)dx等价.

解答如下问题：(1)设{an },{bn}为两个数列，且Bn=b1+b2+⋯+bn，证明：an bn=an Bn+Bk (ak-ak-1)(2)记⁡1/n kxk=A，证明：⁡1/n2 k2 xk=A/2.

反常积分的审敛法

设p为常数，若反常积分lnx/(xp(1-x)1-p) dx收敛，则p的取值范围是【】

讨论sinbx/xλ dx(b≠0)的绝对收敛性和条件收敛性.

求证：J=ln⁡(sinx)dx收敛且J=-π/2 ln2.

证明：广义积分lnx/√x dx收敛.

先说明广义积分dx/(a4+x4 )收敛（a>0是常数），再计算其积分值.

设函数f(x)在[0,+∞)连续、非负，且广义积分f(x)dx收敛，证明：xf(x)dx=0.

证明含参广义积分F(a)=e-axsinxdx在(0,+∞)连续，但非一致收敛.

判断dx/(ex+1)的敛散性.

设[a,+∞)上非负连续函数f可导，且具有连续导函数，若存在r>1，使xf'(x)/f(x)≤-r，证明：反常积分f(x)dx收敛.

求曲面积分∬S(z3-x)dydz-xydzdx-3zdxdy.其中S是由曲面z=4-y2，平面x=0，平面x=3以及xOy平面围成立体的表面，取外侧.

定积分

设f∈[0,2π]，证明：f(x)|sinnx|dx=2/πf(x)dx.

设f(x)在(0,1)可微，且有x2 f(x) dx=0，证明：存在θ∈(0,1)，使得f' (θ)=-f(θ)/θ.

设f(x),g(x)在区间[a,b]上连续，且g(x)取正值，由积分中值定理有f(t)g(t)dt=f(ξ)g(t) dt(a≤ξ≤x≤b)若f+' (a)存在且f+' (a)≠0，求(ξ-a)/(x-a).

当某公司推出一个新的社交软件时，公司的市场部门除了会关心该软件的活跃客的总人数随时间的变化，也会对客户群体的一些特征做具体的调研和分析。我们用n(t,x)表示客户的数量密度(以下简称密度)，这里t表示时间，而x表示客户对该社交软件的使用时长，那么在t时刻，对于0<x1<x2，使用时长介于x1和x2之间的客户数量为n(t,x)dx。我们假设，密度n(t,x)随着时间演化受以下几个因素的影响：假设1.当客户持续使用该社交软件时,他的使用时长随时间线性增长。假设2.客户在使用过程中，可能会停止使用，我们假设停止速率d(x)>0只跟使用时长x有关。假设3.新客户的来源有两个。①公司的宣传：单位时间内因此增加的人数是时间的函数，用c(t)表示。②老客户的宣传：老客户会主动向自己的同事、朋友等推荐使用该社交软件，推荐成功的速率跟客户的使用时长x有关，记作b(x)。假设如果在某一时刻，记为t=0时，密度函数是已知的，n(0,x)=n0 (x)。可以推导出，n(t,x)的时间演化满足如下的方程 (1)这里N(t)可解读为新客户的增加速率。我们假设b,d∈(0,∞)，即b(x)和d(x)正且(本质)有界。以下,我们先做一个简化假设：c(t)≡0，即新客户的增加只跟老客户的宣传有关。(i)问答题(10分)根据假设1和假设2，形式地推导出(1)中n(t,x)所满足的偏微分方程，需要在推导过程中指出模型假设和数学表达式之间的对应关系。再根据假设3，解释(1)中N(t)的定义的含义。(ii)问答题(10分)我们想要研究新客户的增加速率N(t)和推荐成功速率b(x)之间的关系。为此,请推导出一个N(t)所满足的方程，且方程中只包含N(t),n0 (x),b(x),d(x)，而不包含n(t,x)。并证明，N(t)满足如下估计|N(t)|≤‖b‖∞|n0 (x)|dx,这里‖∙‖∞表示L∞范数。(iii)证明题(10分)最后，我们想要研究，在充分长的时间之后，数量密度函数n(t,x)有什么渐近的趋势。由于客户总人数可能一直在增加，所以我们不方便直接研究数量密度函数n(t,x)，而更应该去看一个重整化的密度函数。为此，我们首先假设如下的特征值问题有唯一解(λ0,φ(x))：并且它的对偶问题也有唯一的解ψ(x)：然后，我们定义重整化密度n ̃(t,x)≔n(t,x)e-λ0 t。证明，对于任意凸函数H:R+→R+满足H(0)=0，我们有d/dt ψ(x)φ(x)H()dx≤0,∀t≥0,并证明ψ(x)n(t,x))dx=eλ0t ψ(x) n0 (x)dx.

数值求积f(x)dx时(1)试写出直接用梯形公式的计算式T1；(2)将[a,b]n等分，用Tn表示用复化梯形公式求得的积分值，试写出Tn的计算式；(3)若将步长分半（即步长二分），试给出T2n与Tn的递推关系；(4)若用精度控制|T2n - Tn |<ε，试写出“变步长梯形法”的算法框图.

用Romberge方法求dx的近似值。（给定n=4）

利用留数定理计算下列积分cos(bx)dx（a>0,b为实数）

利用δ函数的性质，计算积分δ(x2+1)sinxdx.

设f(x)在[0,1]上连续，f(x)dx=0,xf(x)dx=1，则存在x0∈[0,1]使|f(x0 )|>4.

求定积分sinθ/(sinθ+cosθ) dθ.