大学数学-考研试题(重庆大学 2003年定积分的分部积分法)

计算题（2003年重庆大学）

求定积分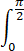sinθ/(sinθ+cosθ) dθ.

答案解析

暂无答案

讨论

大学数学

设函数g(x)在x=0的领域内有定义，g(0)=g'(0)=0,f(x)=，求f'(0).

求极限⁡( - ).

若f(x,y)的偏导数fx,fy在(x0,y0)存在，则f(x,y)在(x0,y0)连续.

设f(x)在[0,+∞)上非负连续，n是正整数，若f(x)dx存在，则f(x)dx收敛.

若|un+1 - un |收敛，则un存在.

若un>0,n=1,2,…且∀n,un+1/un <1则un 收敛.

若f(x,y)在区域D内对x和y都是连续的，则f(x,y)对(x,y)D为二元连续.

定义函数f(x)在[a,b]可积时，必须选假定f(x)在[a,b]上有界.

若f(x),g(x)在[a,b]上可导，∀x∈[a,b],f' (x)≤g'(x)，则∀x∈[a,b],f(x)≤g(x).

若f(x)在x0的领域内有定义，在x0可导，则f(x)在x0的某领域内连续.

定积分的分部积分法

利用留数定理计算下列积分cos(bx)dx（a>0,b为实数）

利用δ函数的性质，计算积分δ(x2+1)sinxdx.

计算积分xm-1/(1+xn) dx，其中0<m<n.

求ln⁡(1+x)/(2-x)2 dx.

tsint dt=__________.

求ln⁡(1+x)/(2-x)2 dx.

设函数f(x)在开区间[0,1]上可微，f(0)=0，且在[0,1]内0<f'(x)<1，证明：(1)对于任意x∈(0,1),f(t)dt>1/2 f2 (x);(2) (f(x)dx)2>f3(x)dx.

设fn (x)在(a,b)上单调递增，且有实数列{Mn },n=1,2,3,…使得∀x∈(a,b),|fn (x)|≤Mn，若fn (x)在(a,b)上一致收敛于f(x)，证明：(1)存在M>0，使得∀x∈(a,b),|f(x)|≤M;(2)极限f(x)存在.

对∀p为正整数，|un+p - un |=0，则un 存在.

定积分

浙江省定积分的换元法

利用δ函数计算下列积分(x2+1)δ(x2-2x-8)dx.

lnx/√x dx=__________.

证明：sin⁡(x²)dx>0.

求定积分x(sinx)arctan⁡(e-x)/(1+cos2⁡x )dx

设连续函数f(x)满足f(x+2)-f(x)=x,f(x)dx=0，则f(x)dx=______.

设x,t>0，则含参变量积分I(t)=(e-x -e-xt)/x dx=________.

设连续函数f(x)满足f(a+b-x)=f(x),∀x∈[a,b]，则积分xf(x)dx等于【】

南京大学定积分的概念与性质