求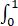 ln(1+x)/(2-x)2 dx.
ln(1+x)/(2-x)2 dx.
计算题(1990年理工数学Ⅰ)
答案解析
原式=ln(1+x)d(1/(2-x))= 1/(2-x) ln(1+x)-dx/(1+x)(2-x) =ln2-1/3 (1/(2-x)+1/(1+x)) dx =ln2-1/3 ln...
查看完整答案讨论
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解,α1,α2是对应齐次线性方程组Ax=0的基础解系,k1,k2为任意常数,则方程组Ax=b的通解(一般解)必是【 】
已知f(x)在x=0的某个领域内连续,且f(0)=0,f(x)/(1-cosx)=2,则在点x=0处f(x)【 】
已知函数f(x)具有任意阶导数,且f' (x)=[f(x)]2,则当n为大于2的正整数时,f(x)的n阶导数f(n) (x)等于【 】
设f(x)是连续函数,且F(x)=f(t)dt,则F'(x)等于【 】
已知离散型随机变量X服从参数为2的泊松分布,即P{X=k}=2ke-2/k!,k=0,1,2,…,则随机变量Z=3X-2的期望E(Z)=________.
设随机事件A,B及其和事件A∪B的概率分别是0.4,0.3,0.6,若B ̅表示B的对立事件,那么积事件AB ̅的概率P(AB ̅ )=________.
已知随机变量X的概率密度函数f(x)=1/2 e-|x|,-∞<x<+∞,则X的概率分布函数F(x)=____________.
已知向量组α1=(1,2,3,4),α2=(2,3,4,5),α3=(3,4,5,6),α4=(4,5,6,7),则该向量组的秩是______.
设函数f(x)在[0,+∞)连续、非负,且广义积分f(x)dx收敛,证明:xf(x)dx=0.
证明含参广义积分F(a)=e-axsinxdx在(0,+∞)连续,但非一致收敛.
f(x)在[0,1]上有连续导数,f(x)无零点,且f(0)=1,f(1)=2,则dx= __________。
设f(x)在[0,1]上连续,f(x)dx=0,xf(x)dx=1,则存在x0∈[0,1]使|f(x0 )|>4.
设f(x)连续,且f(t)dt=x,则f(7)=______.
设f(x)是连续函数,且f(x)=x+2f(t)dt=________.

