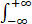 |x|
|x|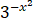 dx = ______.
dx = ______.
已知矩阵A=,若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵,则P,Q可以分别取【 】
设3阶矩阵A=(α1,α2,α3),B=(β1,β2,β3),若向量组α1,α2,α3可以由向量组β1,β2线性表出,则【 】
设函数f(x)=secx在x=0处的2次泰勒多项式为1+ax+bx2,则【 】
设函数f(x)=ax-blnx(a>0)有两个零点,则b/a的取值范围是【 】
有一圆柱体底面半径与高随时间变化的速率分别为2cm/s,-3cm/s,当底面半径为10cm,高为5cm时,圆柱体的体积与表面积随时间变化的速率分别为【 】
在区间(0,2)上随机取一点,将该区间分成两段,较短的一段长度记为X,较长的一段记为Y,令Z=Y/X.(1) 求X的概率密度;(2) 求Z的概率密度;(3) 求E(X/Y).
已知A=(1) 求正交矩阵P,使得PTAP为对角矩阵;(2) 求正定矩阵C,使得C2 = (a+3)E-A.
设D⊂R2是有界单连通闭区域,I(D)=(4-x2-y2)dxdy取得最大值的积分区域记为D1.(1) 求I(D1 )的值.(2) 计算,其中∂D1是D1的正向边界.
计算(e-ax - e-bx)/x sinxdx,其中a,b>0.
设f(x)连续,且f(t)dt=x,则f(7)=__________.
设f(x)在(-∞,+∞)内连续可导,且m≤f(x)≤M,a>0.(1)求1/(4a2)[f(t+a)-f(t-a)]dt;(2)求证:|1/2af(t)dt-f(x)|≤M-m.
f(x)在[0,1]上有连续导数,f(x)无零点,且f(0)=1,f(1)=2,则dx= __________。
已知二次型f(x1,x2,x3 )=3x12+4x22+3x32+2x1 x3,(1)求正交变换x=Qy将f(x1,x2,x3)化为标准形;(2)证明minx≠0f(x)/(xT x)=2.

