设f(x)在(-∞,+∞)内连续可导,且m≤f(x)≤M,a>0.
(1)求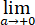 1/(4a2)
1/(4a2)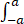 [f(t+a)-f(t-a)]dt;
[f(t+a)-f(t-a)]dt;
(2)求证:|1/2a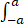 f(t)dt-f(x)|≤M-m.
f(t)dt-f(x)|≤M-m.
设f(x)在(-∞,+∞)内连续可导,且m≤f(x)≤M,a>0.
(1)求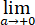 1/(4a2)
1/(4a2)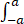 [f(t+a)-f(t-a)]dt;
[f(t+a)-f(t-a)]dt;
(2)求证:|1/2a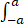 f(t)dt-f(x)|≤M-m.
f(t)dt-f(x)|≤M-m.
(1)因为f(x)在(-∞,+∞)上有连续导数,由积分中值定理知存在ξ∈(-a,a),使1/(4a2 ) [f(t+a)-f(t-a)] dt=1/(4a2 )∙[f(ξ+a)-f(ξ-a)]∙2a =1/2a∙[f(ξ+a)-f(ξ-a)],又由题设知f(x)在[ξ-a,ξ+a]上满足拉格朗日中值定理的条件,因此存在η∈(ξ-a,ξ+a),使1/2a∙[f(ξ+...
查看完整答案积分中值定理的条件是__________,结论是____________.
设f(x)是连续函数,且F(x)=f(t)dt,则F'(x)等于【 】
设函数f(x)在[0,1]上连续,在(0,1)内可导,且3f(x)dx=f(0),证明:在(0,1)内存在一点c,使f'(c)=0.
证明:xasinxdx∙a-cosx dx≥π³/4其中,a>0为常数.
设f(a)=0,f(x)在[a,b]上的导数连续,求证:1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] |f'(x)|,x∈[a,b]
设f(x)在(0,1)可微,且有x2 f(x) dx=0,证明:存在θ∈(0,1),使得f' (θ)=-f(θ)/θ.
设I1=x/2(1+cosx) dx,I2=ln(1+x)/(1+cosx) dx,I3=2x/(1+sinx) dx,则【 】