-
关注“优题吧”，分配平台账号.
题吧，智能辅助学习中心
考研2025年理工数学Ⅰ( )
计算
1/((x+1)(x²-2x+2)) dx.
解答过程见word版
考研2024年北京邮电大学( )
判别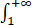
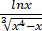dx的敛散性.
解答过程见word版
考研2024年北京邮电大学( )
计算定积分：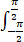
(1+sin(3x))/(1+cos²x ) dx.
解答过程见word版
考研2024年武汉大学( )
证明：(xlnx)ndx=(-1)nn!/(n+1)n+1 ，并利用此结论证明：x-x dx=
1/nn .
考研2024年武汉大学( )
用含参量积分求arctanx/x
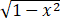dx