大学数学-考研试题(北京邮电大学 2024年反常积分的审敛法)

问答题（2024年北京邮电大学）

判别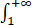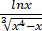dx的敛散性.

答案解析

解答过程见word版

讨论

大学数学

当x→0时，xe-x/2与αxn是等价无穷小，求α和n.

讨论方程(lnx)²-2lnx+2x+k=0的实根的个数，其中k是常数.

证明：若an>0,an/an+1 =l>1，则an=0.

求二元函数f(x,y)=x²(2+y²)+ylny的极值.

求幂级数(-1)n-1/(2n-1) x2n的收敛域及和函数.

计算定积分：(1+sin⁡(3x))/(1+cos²⁡x ) dx.

北京邮电大学泰勒公式

设{fn(x)}是区间[a,b]上一致收敛于f的可积函数列，证明：f在[a,b]上可积，且f(x)dx=fn(x) dx.

证明：(xlnx)ndx=(-1)nn!/(n+1)n+1 ，并利用此结论证明：x-x dx=1/nn .

设x>0,y>0，证明：xy-ex-1≤ylny

反常积分的审敛法

设函数f是(0,1]上无界的单调函数，且广义积分f(x) dx收敛，证明：1/n f((k-1)/n) =f(x)dx

证明含参广义积分F(a)=e-axsinxdx在(0,+∞)连续，但非一致收敛.

设[a,+∞)上非负连续函数f可导，且具有连续导函数，若存在r>1，使xf'(x)/f(x)≤-r，证明：反常积分f(x)dx收敛.

设p为常数，若反常积分lnx/(xp(1-x)1-p) dx收敛，则p的取值范围是【】

讨论sinbx/xλ dx(b≠0)的绝对收敛性和条件收敛性.

求证：J=ln⁡(sinx)dx收敛且J=-π/2 ln2.

证明：广义积分lnx/√x dx收敛.

先说明广义积分dx/(a4+x4 )收敛（a>0是常数），再计算其积分值.

求积分I(a)=arctan⁡(ax)/(x(1+x2)) dx,a>0.

判断dx/(ex+1)的敛散性.

定积分

计算(1/t-[1/t]) dt

设函数f(x)=sint3dt,g(x)=f(t)dt，则【】

设函数f(x)=ecostdt,g(x)=et² dt，则【】

设I=|sinx|dx,k为整数，则I的值【】

5/(x4+3x2-4)dx__________.

证明：1/T sinatcosbt/t dt=

求含参积分I(y)=e-x²cos⁡(2xy) dx.

计算e-1/4s s-3/2e-s ds

用含参量积分求arctanx/x dx

e√x =__________.