大学数学-考研试题(安徽大学 2024年微积分基本公式)

计算题（2024年安徽大学）

求含参积分I(y)=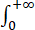e^-x²cos⁡(2xy) dx.

答案解析

暂无答案

讨论

大学数学

计算Gauss曲面积分I=∬Scos⁡((n,r) ̂)/r² dS，其中S为光滑封闭曲面，原点不在S上，r为S上动点至原点的距离，(n,r) ̂为动点处外法向量n与径向r的夹角.

给定方程x²+y + sin(xy)=0.(1) 说明在点(00)的充分小的邻域内，此方程确定唯一的可导的函数 y=y(x)，使得 y(0)= 0，并求出 y=y(x)的导函数表达式.(2) 判断在点(0,0)的充分小的邻域内，此方程是否确定唯一的函数 x =x(y)，使得x(0)=0，说明理由.

设f(n)=a0+ak/nk ，且满足|a_k |≤M，这里n,k均为正整数，试证：数项级数f(n)收敛的充要条件为a0=a1=0.

设函数f(x)为(a,b)上的凸函数，即∀x1,x2∈(a,b)以及λ∈(0,1)，有f(λx1+(1-λ) x2 )≤λf(x1 )+(1-λ)f(x2)证明：(1)对∀x∈(a,b)，左右导数f-' (x),f+' (x)均存在，且f-' (x)≤f+' (x)，(2) f-' (x),f+' (x)均在(a,b)上单调递增.

设函数f(x)在I上有定义，令ωf(δ)=|f(x)-f(y)|证明：(1)ωf(δ)存在.(2) f(x)在区间I上一致连续等价于ωf(δ)=0.

设数列{xn}有界，且(xn+1-xn)=0，令 m=xn ,M=xn,m<M证明：在区间(m,M)上任意一个数都是此数列的一个子列的极限.

求极限：[1/e (1+1/x)x ]x

求极限：⁡n[(1²+3²+⋯+(2n+1)²)/n³ -4/3]

设函数f在[0,1]上连续，定义g(t)=(tf(x))/(x²+t²) dx,t∈R证明：函数g在点0处连续当且仅当f(0)=0.

设函数f在R上可微，且满足对任意x∈R，有f(x+1)-f(x)=f'(x)以及f' (x)=1，证明：存在常数C，使得f(x)=x+C.

定积分

计算(1/t-[1/t]) dt

设函数f(x)=sint3dt,g(x)=f(t)dt，则【】

设函数f(x)=ecostdt,g(x)=et² dt，则【】

设I=|sinx|dx,k为整数，则I的值【】

5/(x4+3x2-4)dx__________.

证明：1/T sinatcosbt/t dt=

设函数f是(0,1]上无界的单调函数，且广义积分f(x) dx收敛，证明：1/n f((k-1)/n) =f(x)dx

lnx/√x dx=__________.

计算积分xm-1/(1+xn) dx，其中0<m<n.

用Romberge方法求dx的近似值。（给定n=4）

微积分基本公式

设f(x)连续，且f(t)dt=x，则f(7)=__________.

理工数学Ⅱ微积分基本公式

(2x+3)/(x2-x+1)dx=__________.

计算(e-ax - e-bx)/x sinxdx，其中a,b>0.

计算积分ln⁡(1-2acosx+a2)dx.

设f(x)在(-∞,+∞)内连续可导，且m≤f(x)≤M,a>0.(1)求1/(4a2)[f(t+a)-f(t-a)]dt;(2)求证：|1/2af(t)dt-f(x)|≤M-m.

f(x)在[0,1]上有连续导数，f(x)无零点，且f(0)=1,f(1)=2，则dx= __________。

|x|dx = ______.

积分2/(x2+2x+4) dx=__________.