大学数学-考研试题(西安交通大学 2024年微积分基本公式)

证明题（2024年西安交通大学）

证明：

1/T 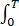sinatcosbt/t dt=

答案解析

暂无答案

讨论

定积分

计算(1/t-[1/t]) dt

设函数f(x)=sint3dt,g(x)=f(t)dt，则【】

设函数f(x)=ecostdt,g(x)=et² dt，则【】

设I=|sinx|dx,k为整数，则I的值【】

5/(x4+3x2-4)dx__________.

利用δ函数的性质，计算积分δ(x2+1)sinxdx.

求定积分sinθ/(sinθ+cosθ) dθ.

设函数f(x)在[0,+∞)连续、非负，且广义积分f(x)dx收敛，证明：xf(x)dx=0.

证明含参广义积分F(a)=e-axsinxdx在(0,+∞)连续，但非一致收敛.

若f(x)为已知连续函数，I=tf(tx)dx，其中t>0,s>0，则I的值【】

无穷小与无穷大

当x→0+时，下列无穷小阶数最高的是【】

当x→0时，((1+t²)sint²)/(1+cost²) dt与xk是等阶无穷小，则k=______.

当x→0时，α(x),β(x)是非零无穷小量，给出以下四个命题①若α(x)~β(x)，则α2 (x)~β2 (x)②若α2 (x)~β2 (x)，则α(x)~β(x)③若α(x)~β(x)，则α(x)-β(x)=o(α(x))④若α(x)-β(x)=o(α(x))，则α(x)~β(x)其中所有真命题的序号是【】

当x→0时，函数f(x)=ax+bx2+ln⁡(1+x)与g(x)=ex^2 -cosx是等价无穷小，则ab=______.

已知{xn },{yn}满足x1=yn=1/2,xn+1=sinxn,yn+1=yn2 (n=1,2,⋯) ，则当n→∞时【】

设f(x)有连续的导数，f(0)=0,f'(0)≠0,F(x)=(x2-t2) f(t)dt，且当x→0时，F'(x)与xk是同阶无穷小，则k等于【】

已知当x→0时，(1+ax2)1/3-1与cosx-1是等价无穷小，则常数a=__________.

当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【】

设a≠，则ln= .

当x→0时，(-1)dt是x7的【】

微积分基本公式

设f(x)连续，且f(t)dt=x，则f(7)=__________.

理工数学Ⅱ微积分基本公式

(2x+3)/(x2-x+1)dx=__________.

计算(e-ax - e-bx)/x sinxdx，其中a,b>0.

计算积分ln⁡(1-2acosx+a2)dx.

设f(x)在(-∞,+∞)内连续可导，且m≤f(x)≤M,a>0.(1)求1/(4a2)[f(t+a)-f(t-a)]dt;(2)求证：|1/2af(t)dt-f(x)|≤M-m.

f(x)在[0,1]上有连续导数，f(x)无零点，且f(0)=1,f(1)=2，则dx= __________。

|x|dx = ______.

积分2/(x2+2x+4) dx=__________.