大学数学-考研试题(北京邮电大学 2024年定积分的概念与性质)

计算题（2024年北京邮电大学）

计算定积分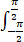：(1+sin⁡(3x))/(1+cos²⁡x ) dx.

答案解析

解答过程见word版

讨论

大学数学

北京邮电大学泰勒公式

设{fn(x)}是区间[a,b]上一致收敛于f的可积函数列，证明：f在[a,b]上可积，且f(x)dx=fn(x) dx.

证明：(xlnx)ndx=(-1)nn!/(n+1)n+1 ，并利用此结论证明：x-x dx=1/nn .

设x>0,y>0，证明：xy-ex-1≤ylny

设f(x)是[-1,1]上的连续函数，证明：⁡εf(x)/(ε²+x²)dx=πf(0)

设f(x)在(0,+∞)上三次可导，且f(x)与f'''(x)均存在，证明：⁡f' (x)=⁡f'' (x)=f'''(x)=0

证明：2n/(2n+1)≤(1+1/n)n/e≤(2n+1)/(2n+2)(n≥1)

用含参量积分求arctanx/x dx

求曲面积分∬S(xy+yz+zx)dS其中S是z=被x²+y²=2ay截掉的部分.

以x=ty参数化曲线x²+y³=xy，求曲线所围区域的面积.

定积分

计算(1/t-[1/t]) dt

设函数f(x)=sint3dt,g(x)=f(t)dt，则【】

设函数f(x)=ecostdt,g(x)=et² dt，则【】

设I=|sinx|dx,k为整数，则I的值【】

5/(x4+3x2-4)dx__________.

证明：1/T sinatcosbt/t dt=

设函数f是(0,1]上无界的单调函数，且广义积分f(x) dx收敛，证明：1/n f((k-1)/n) =f(x)dx

求含参积分I(y)=e-x²cos⁡(2xy) dx.

计算e-1/4s s-3/2e-s ds

北京邮电大学反常积分的审敛法

定积分的概念与性质

当某公司推出一个新的社交软件时，公司的市场部门除了会关心该软件的活跃客的总人数随时间的变化，也会对客户群体的一些特征做具体的调研和分析。我们用n(t,x)表示客户的数量密度(以下简称密度)，这里t表示时间，而x表示客户对该社交软件的使用时长，那么在t时刻，对于0<x1<x2，使用时长介于x1和x2之间的客户数量为n(t,x)dx。我们假设，密度n(t,x)随着时间演化受以下几个因素的影响：假设1.当客户持续使用该社交软件时,他的使用时长随时间线性增长。假设2.客户在使用过程中，可能会停止使用，我们假设停止速率d(x)>0只跟使用时长x有关。假设3.新客户的来源有两个。①公司的宣传：单位时间内因此增加的人数是时间的函数，用c(t)表示。②老客户的宣传：老客户会主动向自己的同事、朋友等推荐使用该社交软件，推荐成功的速率跟客户的使用时长x有关，记作b(x)。假设如果在某一时刻，记为t=0时，密度函数是已知的，n(0,x)=n0 (x)。可以推导出，n(t,x)的时间演化满足如下的方程 (1)这里N(t)可解读为新客户的增加速率。我们假设b,d∈(0,∞)，即b(x)和d(x)正且(本质)有界。以下,我们先做一个简化假设：c(t)≡0，即新客户的增加只跟老客户的宣传有关。(i)问答题(10分)根据假设1和假设2，形式地推导出(1)中n(t,x)所满足的偏微分方程，需要在推导过程中指出模型假设和数学表达式之间的对应关系。再根据假设3，解释(1)中N(t)的定义的含义。(ii)问答题(10分)我们想要研究新客户的增加速率N(t)和推荐成功速率b(x)之间的关系。为此,请推导出一个N(t)所满足的方程，且方程中只包含N(t),n0 (x),b(x),d(x)，而不包含n(t,x)。并证明，N(t)满足如下估计|N(t)|≤‖b‖∞|n0 (x)|dx,这里‖∙‖∞表示L∞范数。(iii)证明题(10分)最后，我们想要研究，在充分长的时间之后，数量密度函数n(t,x)有什么渐近的趋势。由于客户总人数可能一直在增加，所以我们不方便直接研究数量密度函数n(t,x)，而更应该去看一个重整化的密度函数。为此，我们首先假设如下的特征值问题有唯一解(λ0,φ(x))：并且它的对偶问题也有唯一的解ψ(x)：然后，我们定义重整化密度n ̃(t,x)≔n(t,x)e-λ0 t。证明，对于任意凸函数H:R+→R+满足H(0)=0，我们有d/dt ψ(x)φ(x)H()dx≤0,∀t≥0,并证明ψ(x)n(t,x))dx=eλ0t ψ(x) n0 (x)dx.

数值求积f(x)dx时(1)试写出直接用梯形公式的计算式T1；(2)将[a,b]n等分，用Tn表示用复化梯形公式求得的积分值，试写出Tn的计算式；(3)若将步长分半（即步长二分），试给出T2n与Tn的递推关系；(4)若用精度控制|T2n - Tn |<ε，试写出“变步长梯形法”的算法框图.

用Romberge方法求dx的近似值。（给定n=4）

设f(x)在[0,1]上连续，f(x)dx=0,xf(x)dx=1，则存在x0∈[0,1]使|f(x0 )|>4.

设f(x)连续，且f(t)dt=x，则f(7)=______.

设f(x)是连续函数，且f(x)=x+2f(t)dt=________.

积分中值定理的条件是__________，结论是____________.

f'(2x)dx=__________.

设f(x)是连续函数，且F(x)=f(t)dt，则F'(x)等于【】

设函数f(x)在[0,1]上连续，在(0,1)内可导，且3f(x)dx=f(0)，证明：在(0,1)内存在一点c，使f'(c)=0.