大学数学-考研试题(北京邮电大学 2024年泰勒公式)

计算题（2024年北京邮电大学）

求极限：

答案解析

解答过程见word版

讨论

大学数学

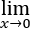
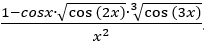
设{fn(x)}是区间[a,b]上一致收敛于f的可积函数列，证明：f在[a,b]上可积，且f(x)dx=fn(x) dx.

证明：(xlnx)ndx=(-1)nn!/(n+1)n+1 ，并利用此结论证明：x-x dx=1/nn .

设x>0,y>0，证明：xy-ex-1≤ylny

设f(x)是[-1,1]上的连续函数，证明：⁡εf(x)/(ε²+x²)dx=πf(0)

设f(x)在(0,+∞)上三次可导，且f(x)与f'''(x)均存在，证明：⁡f' (x)=⁡f'' (x)=f'''(x)=0

证明：2n/(2n+1)≤(1+1/n)n/e≤(2n+1)/(2n+2)(n≥1)

用含参量积分求arctanx/x dx

求曲面积分∬S(xy+yz+zx)dS其中S是z=被x²+y²=2ay截掉的部分.

以x=ty参数化曲线x²+y³=xy，求曲线所围区域的面积.

求极限 sin⁡(k/n)∙sin(k/n²)

泰勒公式

设f(x)在[0,1]上具有二阶导数，且满足条件|f(x)|≤a,|f''(x)|≤b，其中a,b都是非负常数，c是(0,1)内任意一点，证明：|f'(c)|≤2a+b/2.

已知f(x)在[a,b]上二阶可导，且f''(x)≤0，证明：f(x)dx≤(b-a)f((a+b)/2).

设x>0时，f(x)=，求证：x→0+时，f(x)=e+Ax+Bx2+o(x2)，并求A,B之值.

当x→0时，1-cosxcos2xcos3x对于无穷小x的阶数等于 __________.

设函数f(x)=sinx/(1+x2)在x=0处的3次泰勒多项式为ax+bx2+cx3，则【】

当x→0时，x-sinxcosxcos2x与cx4为等价无穷小，则c=__________，k=__________.

设函数f(x)在区间[0,1]上连续，则f(x)dx=【】

设函数f(x)=secx在x=0处的2次泰勒多项式为1+ax+bx2，则【】

计算定积分：(1+sin⁡(3x))/(1+cos²⁡x ) dx.

求幂级数(-1)n-1/(2n-1) x2n的收敛域及和函数.

中值定理与导数的应用

设f(x)在[0,2]上具有连续导数，f(0)=f(2)=0,M=max⁡|f(x)|,x∈[0,2]，证明：(1)∃ξ∈[0,2]，使得|f'(ξ)|≥M；(2)若∀x∈[0,2],|f'(x)|≤M，则M=0.

设函数f:[0,1]→R是连续的且在(0,1)上可微，若f满足：(1) f(0)=0；(2)存在常数M>0使得|f'(x)|≤M|f(x)|对任意x∈(0,1)成立.证明：在[0,1]上f(x)=0.

曲线y²=x在点(0,0)处的曲率圆方程为____________________.

函数f(x,y)=2x³-9x²-6y4+12x+24y的极值点是__________.

设函数f(x)具有2阶导数，且f' (0)=f' (1),|f'' (x)|≤1，证明：(1)当x∈(0,1)时，|f(x)-f(0)(1-x)-f(1)x|≤(x(1-x))/2;(2) |f(x) dx-(f(0)+f(1))/2|≤1/12.

某产品的价格函数为p=，（p为单价，单位：万元；Q为产量，单位：件），总成本函数为C=150+5Q+0.25Q²（万元），则经营该产品可获得的最大利润为______(万元).

设函数f(x)为(a,b)上的凸函数，即∀x1,x2∈(a,b)以及λ∈(0,1)，有f(λx1+(1-λ) x2 )≤λf(x1 )+(1-λ)f(x2)证明：(1)对∀x∈(a,b)，左右导数f-' (x),f+' (x)均存在，且f-' (x)≤f+' (x)，(2) f-' (x),f+' (x)均在(a,b)上单调递增.

数列{n√n}(n=1,2,3,⋯)的最大项为5√5.

已知方程a1/(x-λ1 )+a2/(x-λ2 )+a3/(x-λ3 )=0其中a1,a2,a3>0,λ1<λ2<λ3.证明：此方程在区间(λ1,λ2)和(λ2,λ3)中各有一根.

设f(x)=(x-x0 )n φ(x)，其中n为正整数，φ(x)在x0连续且φ(x0 )≠0，讨论f(x)在x0处能否取极值？